Hace unos días recibí esto,

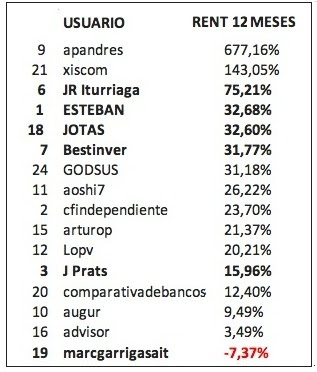
que es la rentabilidad de carteras de inversión (sospecho que no necesariamente reales) de usuarios de cierto portal que compiten por ver quién tiene más ojo en bolsa.

¿No os llama la atención esa rentabilidad >600%? ¿Cómo se puede alcanzar? ¿Es ese señor —a quien no conozco— un hacha de las inversiones?

Dos ideas me vienen a la cabeza. Una es esta que, pienso, no aplica. Y no lo hace porque, en particular, y como ya escribí, la apuesta de Kelly maximiza la mediana de las ganancias, pero ignora su varianza. Que, por lo que veremos luego, es el quid de la cuestión.

Hoy voy a proponer un pequeño problema de geometría elemental: averiguar a qué distancia está el horizonte. Por concretar, supongamos que mides, p.e., 175 cm, estás en la orilla del mar y miras hacia el horizonte. A cierta distancia, la curvatura de la tierra (que tiene un radio de 6378 km) oculta lo que está más allá.

¿Cuál es dicha distancia?

Una complicación adicional: ¿a qué distancia dejaría de verse un barco que tiene una altura de 20 m?

Efectivamente, 44 años después de que Tukey describiese su schematic plot, los diagramas de caja no han calado en el gran público. Dado que dichos diagramas son la representación más simple que se me ocurre de una distribución de probabilidad, me temo que es síntoma de un mal mayor: que no estamos preparados para aceptar que los fenómenos no están perfectamente parametrizados y sino sujetos a errores, oscilaciones, perturbaciones, errores e imprevistos.

Los censos huelen a naftalina. Eso de ir contando exhaustivamente cabezas, críos, cabras y cabañas ya lo hacía el rey David en su época.

Tampoco son operaciones no pequeñas. El último censo chino movilizó a seis millones de encuestadores y el de EE.UU. costó casi como el AVE a Valencia.

Sin embargo, eso de contar sin excepciones es un ejercicio de fuerza bruta propio de la oscura época pre-estadística. El progreso ha traído consigo dos cosas —buena la una, regular la otra—, que permiten replantear enteramente los censos.

Nos encantan las palabras (¡y los mapas, pero esa es otra historia!). En estos días de tanto discurso hay mucho interés por examinar con lupa qué palabras dijo quién y cuándo en una exégesis cuantitativa y (¿tal vez por eso?) falta de calado.

Porque lo que dijo este o aquel, al fin y al cabo, no deja de ser predecible y poco interesante. Rara vez se dice nada que lo sea en horario de máxima audiencia y en fechas tan señaladas.

El primero es How to display data badly, de H. Wainer. Es un poco viejo, de 1984; pero, desgraciadamente, tan vigente si no más. Trata, como puede preverse, del mismo y ya algo manido tema: cómo crear gráficos que representen datos clara y eficazmente. Se agradece que el autor, no sin ironía, lo haya planteado a modo de recetario para conseguir justo lo contrario.

El segundo, Visualizing the Law: Using Charts, Diagrams, and Other Images to Improve Legal Briefs, de A. Rosman, es una lectura de evasión para quien comparta mis obsesiones y frustraciones: la vida me ha llevado a tener que leer —y peor aún, necesitar entender— párrafos de los que redactan leguleyos de toda índole y condición. ¿Es necesario que esa gente se explique así? ¿Habría otra manera? Pues la hay: el artículo en cuestión muestra mediante ejemplos cómo determinados pasajes del género legal pueden desenmarañarse trascendiendo la unidimensionalidad del texto corrido y mal empleado si se usan o, al menos, se acompañan de, los gráficos adecuados.

El problema fue sugerido por Eloy Ortiz en un mensaje a r-help-es. Quería saber cómo muestrear aleatoriamente (i.e., uniformemente) puntos sobre una región de la superficie terrestre delimitada por su bounding box (i.e., las coordenadas que definen un rectángulo sobre la esfera).

Obviamente, no vale con muestrear latitud y longitud uniformemente: el área comprendida entre dos meridianos cerca del ecuador es mayor que la comprendida entre otros dos más próximos al polo. Los husos se estrechan lejos del ecuador.

Pues no lo sé. Seguramente, nadie. Pero como he visto esto (que no es otra forma que una representación palabrera de una matriz de transiciones de Markov) y el debate R vs Python para el análisis de datos ha resonado estos últimos días con cierta fuerza, voy a ensayar un pequeño divertimento matemático que me traslada a una clase práctica de Álgebra I en mis años de estudiante.

Es el siguiente:

# creo la matriz de transición
cols <- c("r", "python", "otros")
mt <- c(227, 108, 33, 31, 140, 7, 58, 27, 68 + 73)
mt <- matrix(mt, nrow = 3, byrow = T)
colnames(mt) <- rownames(mt) <- cols
mt <- prop.table(mt, 1)

# la diagonalizo
tmp <- eigen(mt)

# efectivamente, la diagonalización "funciona"
tmp$vectors %*% diag(tmp$values) %*% solve(tmp$vectors)

# y dejo discurrir 1000 años
tmp$vectors %*% diag(tmp$values^10000) %*% solve(tmp$vectors)

Como resultado, podemos estimar que el en futuro, el 33% de los data scientists estarán usando R contra el 53% que usará Python y el 13% que se decantará por otras herramientas. O, casi seguro, no.

He construido el mapa

porque, a pesar de sus innegables deméritos gráficos, como la profusión de topos rojigualdas, pudiera resultar de interés. No tanto por lo que representa, la distancia de los puntos de la península Ibérica a una lista obsoleta de aeropuertos (en la que no consta, p.e., el de Logroño), sino por el procedimiento que tal vez alguien pueda en su día reaprovechar para un mejor fin.

Hoy, mirando

y tratando de comparar Uruguay y España no he podido dejar de acordarme de