Distribuciones sin media: ¿qué pueden suponer en la práctica?

Aunque esta entrada es sin duda resabida de los más de mis lectores, quedarán los que aún no sepan que ciertas distribuciones no tienen media. Condición necesaria para que una distribución la tenga es que

$$ \int_{-\infty}^\infty |x| f(x) dx$$

tenga un valor finito, cosa que, por ejemplo, no cumple la de Cauchy. Igual hay a quien esto le parece una rareza matemática, un entretenimiento de math kiddies sin implicaciones prácticas. Además, porque para que que la integral anterior diverja se necesita que las distribuciones puedan tomar valores arbitrariamente altos y las que se manejan en la práctica están acotadas si no por el número de átomos del universo por el de céntimos de bolívar venezolano necesarios para comprar todas las cosas que caben en el ancho mundo.

Además, siempre se puede calcular la media empírica de cualquier distribución (con mean en R p.e.). ¿Qué pasa pues si, simplemente, ignorando los caveats matemáticos, vamos y lo tomamos medias? Pues cosas peculiares que comprobará quien corra un código similar a

set.seed(123)
res <- replicate(1000, mean(rcauchy(1e5)))
hist(res, breaks = 50)

es decir, la inestabilidad de esos promedios. Abundando en este caso concreto, debería recordarse que la media de n observaciones independientes de la distribución de Cauchy tiene distribución de Cauchy. Las medias obtenidas no tienen menor dispersión que la de, por ejemplo, la primera observación de cada una de las muestras.

Más aún,

res <- replicate(1000, {
  x <- rcauchy(1e5)
  c(max(x), mean(x))
})

res <- log(abs(t(res)))
colnames(res) <- c("max", "mean")
plot(res)

genera

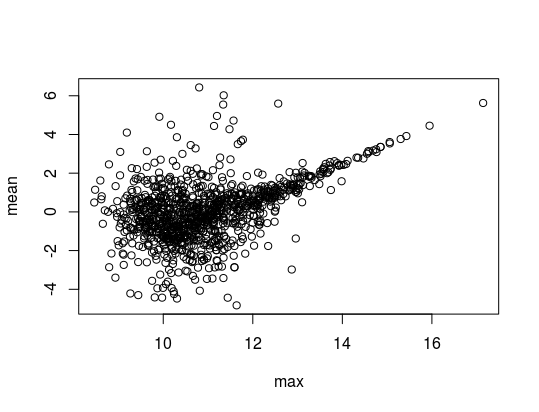
que muestra la dependencia existente en este caso entre la media y el mayor de los valores de la muestra. Dicho de otra manera, la influencia de esta mayor observación en la media muestral.

Ni que decir tiene que no siempre muestreamos distribuciones de Cauchy, pero sí, frecuentemente, con distribuciones con valores extremos. Así que, ¡cuidadín!