Metropolis-Hastings en Scala
Tengo la sensación de que un lenguaje funcional (como Scala) está particularmente bien adaptado al tipo de operaciones que exige MCMC.
Juzguen Vds.
Primero, genero datos en R:
datos <- rnorm(500, 0.7, 1)
writeLines(as.character(datos), "/tmp/datos.txt")Son de una normal con media 0.7. En el modelo que vamos a crear, suponemos conocida (e igual a 1) la varianza de la normal y trataremos de estimar la media suponiéndole una distribución a priori normal estándar. Y con Scala, así:
import scala.io.Source
import java.io.PrintWriter
/* read data */
val source = Source.fromFile("/tmp/datos.txt", "UTF-8")
val data = source.mkString.split("\\s+").map(_.toDouble).toList
/* we need random numbers */
var r = scala.util.Random
/* almost (standard) dnorm */
def dnorm(x:Double): Double = math.exp(-x*x/2)
/* chain transitions */
def rg(y:Double):Double = y + r.nextGaussian
/* prior (standard normal) times likelihood */
def dpost(x:Double): Double = dnorm(x) * data.map(y => dnorm(x - y)).reduce(_*_)
/* metropolis-hastings acceptance ratio */
def acceptanceRatio(from:Double, to:Double):Double = dpost(to) / dpost(from)
def posterior(a:Double):Stream[Double] = {
lazy val elegidos = Stream.continually(a) map rg filter (x => r.nextDouble < acceptanceRatio(a, x))
a #:: posterior(elegidos.head)
}
/* Get values and drop burning obs */
val res = posterior(0.4).take(10000).toList.drop(2000)
/* Thin */
val res_thin = res zip (Stream from 1) filter (_._2 % 5 == 0) map (_._1)
/* Export */
val out = new PrintWriter("/tmp/posterior.txt")
res map out.println
out.close()Leo los datos de la posteriori en R y los represento así:
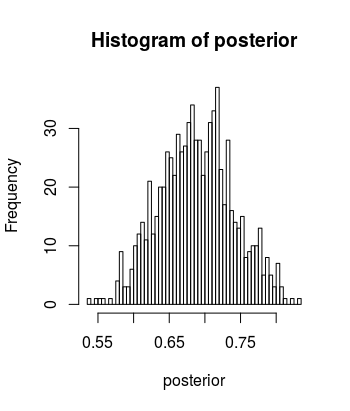
posterior <- as.double(readLines("/tmp/posterior.txt"))
hist(posterior, breaks = 50)