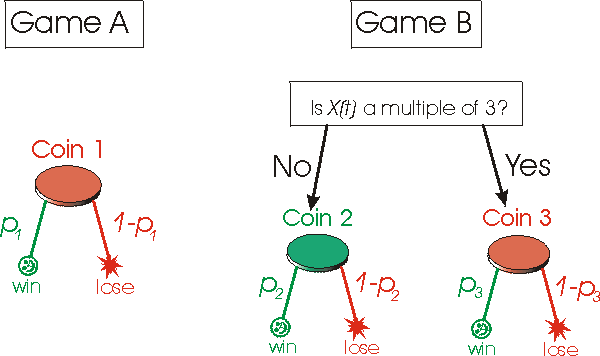Cosa prodigiosa (III): epílogo

Escribo desde mi retiro vacacional, en el hemisferio inhabitual, sin wifis y casi de memoria para completar la historia que comencé hace dos semanas en esta bitácora.

Tropecé con el juego que describí en el libro A Mathematician Plays The Stock Market, de John Allen Paulos. Y creo que se equivoca en las probabilidades de los juegos: si en lugar de las que indiqué en mi primera entrada utilizo las suyas, me da la impresión de que el tercer juego es perdedor. ¿Será un bug en el libro? (¿O es que la dislexia me volvió a confundir?)

Paulos cita a el trabajo del físico español Juan Parrondo , en cuya página hay una discusión muy accesible sobre estos juegos paradójicos así como artículos algo más sesudos sobre el tema.

Y más allá de las referencias y las debidas gentilezas con respecto a mis fuentes, aprovecho de pasada para recordar a mis lectores el concepto de supermartingala y el que podría ser considerado su teorema más importante.

Una martingala es un proceso aleatorio tal que $latex E(X_{n+1} | X_n) = X_n$. Y una supermartingala, uno en el que $latex E(X_{n+1} | X_n) \le X_n$.

¿Extraño? Supóngase que $latex X_n$ es la cantidad acumulada en el juego propuesto. La expresión $latex E(X_{n+1} | X_n)$ es el promedio de las posibles cantidades acumuladas tras jugar $latex n+1$ partidas habida cuenta del resultado de la n-ésima. Por ejemplo, si al cabo de 30 partidas has acumulado 12 euros, $latex (X_{31} | X_{30})$ puede ser 13 euros con probabilidad 0.49 u 11 con probabilidad 0.51 y, por lo tanto, $latex E(X_{31} | X_{30}) = 13 \times 0.49 + 11 \times 0.51 = 11.98 \le 12 = X_{30}$.

De la discusión anterior se deduce que el primer juego es una supermartingala y, si se jugase con una moneda no sesgada, sería una martingala.

Y el teorema fundamental de las martingalas dice que no hay estrategia capaz de vencer a la banca si esta te ofrece participar en un juego que es una supermartingala (como lo es la ruleta, por ejemplo).

Una posible estrategia para vencer al casino sería jugar aleatoriamente a dos juegos distintos, por ejemplo, la ruleta y el nosequé (no soy aficionado a los divertimentos aleatorios: no sé de otros juegos). El teorema demostraría la imposibilidad también de vencer a la banca usando esta estrategia.

¿Y qué de nuestros juegos y, en particular, el tercero? ¿Cómo puede ser que una estrategia que consiste en alternar entre dos juegos perdedores (dos supermartingalas) nos permita vencer a la banca? ¿Fallan las matemáticas?

Por supuesto que no. Y es porque el segundo juego no es una supermartingala: cuando n no es múltiplo de tres, no se cumple $latex E(X_{n+1} | X_n) \le X_n$.

El tercero de los juegos, como consecuencia, es uno de esos ejemplos en que se viola ligeramente las condiciones para que se cumpla el teorema para llegar a una conclusión opuesta a él.

Cierro esta discusión con dos ejercicios para mis lectores:

• Probar que con las probabilidades que se indican en el libro de Paulos, el ejemplo no funciona, i.e., que hay un error en su libro. ¡O no!
• Identificar el otro gran contraejemplo del del teorema del tiempo de espera que se cita por doquier y la ciudad rusa a la que se asocia.