Capítulo 5 Teorema de Bayes
5.1 Teorema de Bayes
En un capítulo anterior, al tratar las probabilidades conjuntas y marginales, se propuso el siguiente modelo probabilístico:
- En un determinado lugar, el 10% de los días llueve y el 90% luce el sol.
- Cuando llueve, la probabilidad de que se produzcan atascos es del 40%.
- Cuando no llueve, la probabilidad de que se produzcan atascos es del 10%.
A partir de esa información, se pudo construir la siguiente tabla de probabilidades conjuntas:
| P(T,A) | atasco | no atasco | P(T) |
|---|---|---|---|
| lluvia | 0.04 | 0.06 | 0.1 |
| sol | 0.09 | 0.81 | 0.9 |
| P(A) | 0.13 | 0.87 | 1 |
Merece la pena prestar atención al hecho de que, por una parte, el modelo probabilístico tiene un orden implícito: del estado del tiempo se deduce —¿podríamos decir que determina?— el del tráfico. Sin embargo, por otra parte, en la tabla de probabilidades conjuntas existe una simetría perfecta entre las dos variables aleatorias involucradas. Viendo dicha tabla uno no sabría si la formulación del problema original es la que es o:
- En un determinado lugar, el \(p_1\)% de los días hay atascos y el \(p_2\)% no.
- Cuando hay atascos, la probabilidad de que esté lloviendo es del \(p_3\)%.
- Cuando no hay atascos, la probabilidad de que esté lloviendo es del \(p_4\)%.
Para ciertos valores \(p_1\), \(p_2\), \(p_3\) y \(p_4\) que pronto se sabrá cómo calcular.
De hecho, en aquella sección y a la vista de la tabla anterior, se planteaba el siguiente problema: de saberse que hay un atasco, ¿cuál sería la probabilidad de que estuviese lloviendo? ¿Y la de que haga sol si no hay atasco? La respuesta a la primera pregunta (que es precisamente \(p_3\) en el párrafo anterior) no es otra cosa que
\[0.04 / 0.13 = .31.\]
En general, llueve el 10% de los días; no obstante, con la información adicional de que hay un atasco, la probabilidad estimada de lluvia crece hasta el 31%.
En este punto, es recomendable recurrir a las llamadas frecuencias naturales (TODO: cita). En la tabla anterior se lee que la probabilidad de atasco es del 13%. Eso significa que de cada 100 días, en 13 hay atasco. De esos 13, en 9 luce el sol y en 4 llueve. La probabilidad buscada es, por tanto, 4 / 13.
TODO: pintar un gráfico a lo Gigerenzer / Spiegelhalter para representar esos valores.
Simbólicamente, por definición,
\[P(T \; | \; A) = \frac{P(T,A)}{P(A)}\]
y tanto \(P(T,A)\) como \(P(A)\) son conocidos. No obstante, se puede obviar la referencia a la probabilidad conjunta desarrollando el numerador \(P(T,A)\) de la forma \(P(T,A) = P(A \; | \; T) P(T)\), con lo que
\[P(T \; | \; A) = \frac{P(A \; | \; T) P(T)}{P(A)}.\]
La expresión anterior se conoce como teorema de Bayes.
En el caso concreto planteado más arriba,
\[P(\text{lluvia} \; | \; \text{atasco}) = \frac{P(\text{atasco} \; | \; \text{lluvia}) P(\text{lluvia})}{P(\text{atasco})} = \frac{0.4 \times 0.1}{0.13} \approx 0.31\]
Este resultado es útil porque, con frecuencia, solo conocemos las probabilidades condicionales menos interesantes. Por ejemplo, nos pueden decir que la sensibilidad de un test para el covid-19 es del 85% y que su especificidad es del 98%. Eso quiere decir que
\[P(\text{test positivo}\;|\; \text{con covid-19}) = .85\]
y que
\[P(\text{test negativo}\;|\; \text{sin covid-19}) = .98.\]
Sin embargo, lo que nos preocupa realmente (por ejemplo, si nuestro test ha resultado positivo) es precisamente
\[P(\text{con covid-19} \;|\; \text{test positivo}),\]
por lo que es necesario utilizar el teorema de Bayes. La siguiente gráfica muestra la probabilidad que estemos realmente afectados por el covid-19 en caso de que nuestra prueba sea positiva:
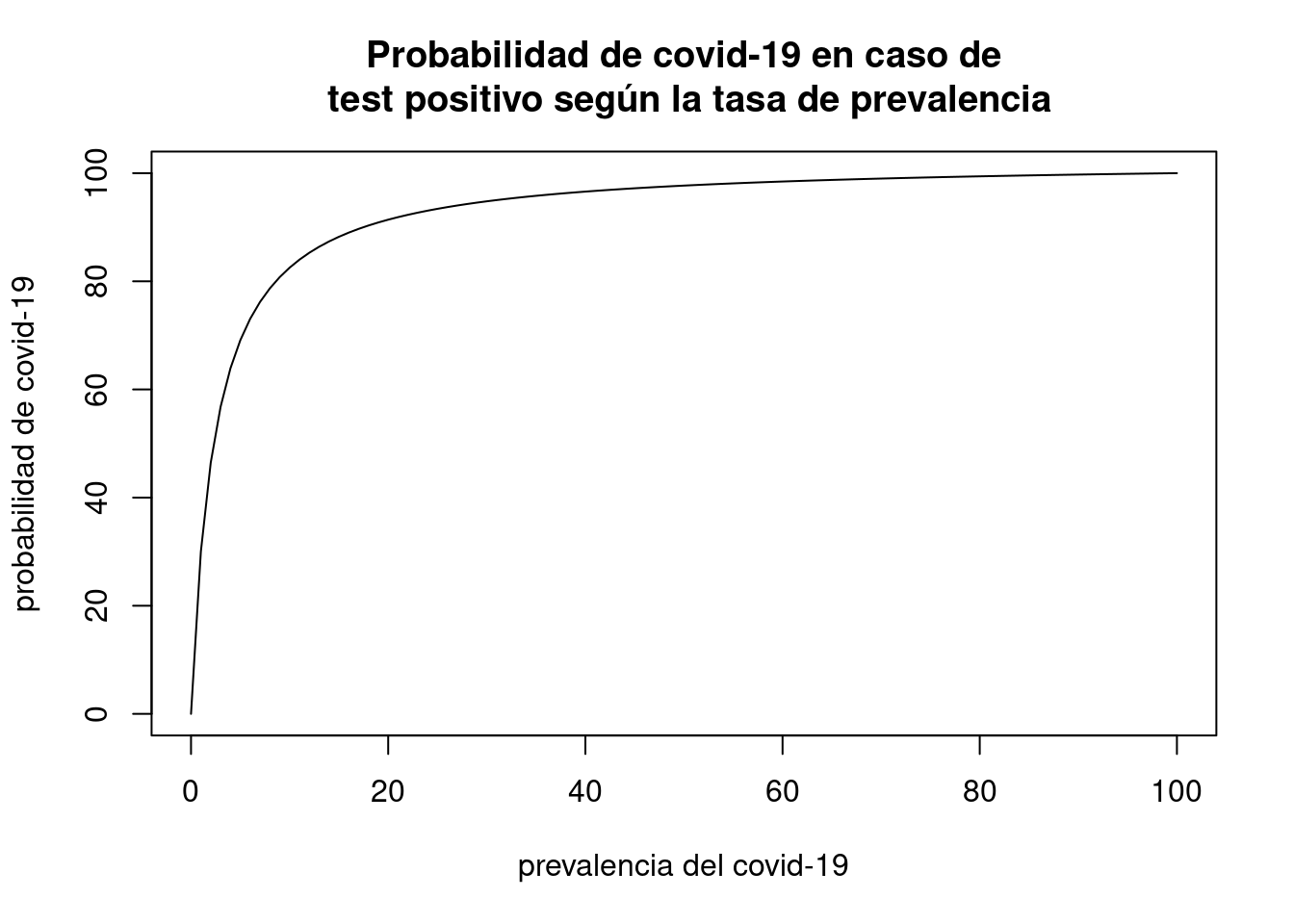
Ejercicio 5.1 Utiliza el teorema de Bayes para escribir la función que se muestra en la figura anterior. Trata luego de implementarla en R para reproducir el gráfico anterior.
Como puede verse, esa probabilidad depende críticamente del nivel de prevalencia. De hecho, cuando esta es baja, casi todos los positivos son falsos: corresponden a ese 2% de positivos que se producen entre la población sana.
5.2 Teorema de Bayes y ciencia de datos
Es difícil infraestimar la importancia del teorema de Bayes en la ciencia de datos. Frecuentemente, uno puede construir expresiones del tipo \(P(D \;|\; \theta)\) que pueden representar lo que se llama un modelo generativo que describe cómo podrían generarse unos datos \(D\) de conocerse unos parámetros \(\theta\). Por ejemplo, \(\theta\) puede representar el CTR (click through rate) de una determinada keyword; por lo tanto, si se conoce \(\theta\) se puede estimar el número de clicks que puede generar en un periodo dado, es decir, \(D\).
Sin embargo, el problema fundamental al que se enfrenta el científico de datos es el inverso: determinar \(\theta\) a partir de los datos observados \(D\). Esto es, determinar \(P(\theta \;|\; D)\).
5.4 Causalidad
La causalidad es el santo grial del científico, incluido el de datos. Lo es porque proporciona mecanismos fiables para provocar efectos deseados. Los textos de teoría de la probabilidad tratan extensamente las relaciones de independencia, apenas las de dependencia y nunca las de causalidad. Esto último sucede porque la probabilidad, como se mostrará en esta sección, no tiene nada que decir acerca de la causalidad en el sentido de que es incapaz de distinguir las relaciones causales de las que no. Pero que sea así no es motivo para no decirlo claramente y desde el principio.
Eso sí, hay que tener en cuenta que la independencia y la causalidad determinista —es decir, aquella que postula que siempre que pasa A, pasa B— son los extremos de un arco de posibles relaciones entre variables aleatorias y, por supuesto, los fenómenos que estas representan.
Desafortunadamente, es muy tentador atribuir mecanismos causales a relaciones de dependencia \(P(A \; | \; B) \ne P(A)\). Así, por ejemplo, al decir que \(P(A \; | \; B) > P(A)\), muchos podrían pensar que \(B\) facilita, fomenta o provoca \(A\). En efecto, hay casos conspicuos en que sucede así: piénsese en el caso en el que \(A\) y \(B\) son determinados tipos de cánceres y el tabaquismo, respectivamente. Sin embargo, esta no es la regla general. Hay que advertir además, que esta problemática (y frecuentemente falsa) atribución de causalidad se realiza tanto al discutir probabilidades condicionales directamente o a través de otras manifestaciones de las probabilidades condicionales más habituales, como por ejemplo, la correlación —que veremos más adelante— o los modelos estadísticos construidos sobre datos observacionales.
El siguiente ejemplo ilustra la cuesión. Se puede argumentar causalmente que la lluvia propicia los atascos, por lo que tiene sentido plantear que \(P(\text{atasco} \; | \; \text{lluvia}) > P(\text{atasco})\) como en el ejemplo discutido en esta sección. Sin embargo, usando el teorema de Bayes, llegamos a la conclusión de que \(P(\text{lluvia} \; | \; \text{atasco}) \ne P(\text{lluvia})\) sin que por ello sea lícito argumentar que los atascos tienen un efecto sobre la meteorología (al menos, en el cortísimo plazo). Si \(P(A \; | \; B) \ne P(A)\) tuviese una lectura del tipo \(B\) causa \(A\), como también podríamos derivar \(P(B \; | \; A) \ne P(A)\), se obtendría un absurdo.
Ejercicio 5.2 Expresa en términos de probabilidades condicionales la siguiente proposición: si conocer \(A\) aumenta la probabilidad de \(B\), entonces el que ocurra \(B\) aumenta la probabilidad de que ocurra \(A\). Además, busca 2 o 3 ejemplos concretos en los que la proposición anterior resulte intuitiva. Finalmente, demuéstrala.
Los neutrinos son unas partículas muy sutiles que prácticamente no interaccionan con la materia y la atraviesan sin dejar apenas rastro. Hacen falta instrumentos muy complejos y costosos para detectar su presencia. De la misma manera, la causalidad atraviesa tanto la teoría de la probabilidad como gran parte (en particular, toda la que se presenta en este libro) de la estadística2 sin que puedan aprehenderla. En realidad, las probabilidades condicionales y los modelos estadísticos (que, como se verá, están muy relacionados con las probabilidades condicionales), predican sobre flujos de información. Así, el que llueva proporciona información sobre el posible estado de las calles; pero, a la inversa, el estado del tráfico puede proporcionar información sobre las condiciones meteorológicas. Conocer las causas modifica nuestra percepción de la probabilidad de los efectos; pero a la inversa, la observación de unos efectos proporciona información sobre la plausibilidad de sus posibles causas.
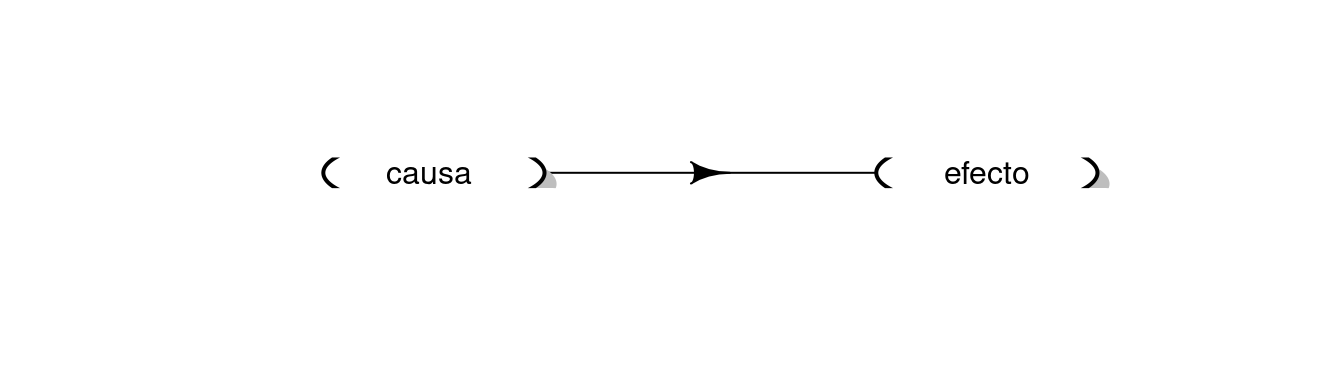
Nótese además cómo la discusión anterior aplica a parejas de variables entre las que existen relaciones de causalidad como en el siguiente diagrama.
Sin embargo, es posible (y, de hecho, es frecuente) encontrar otras configuraciones causales, como estas:
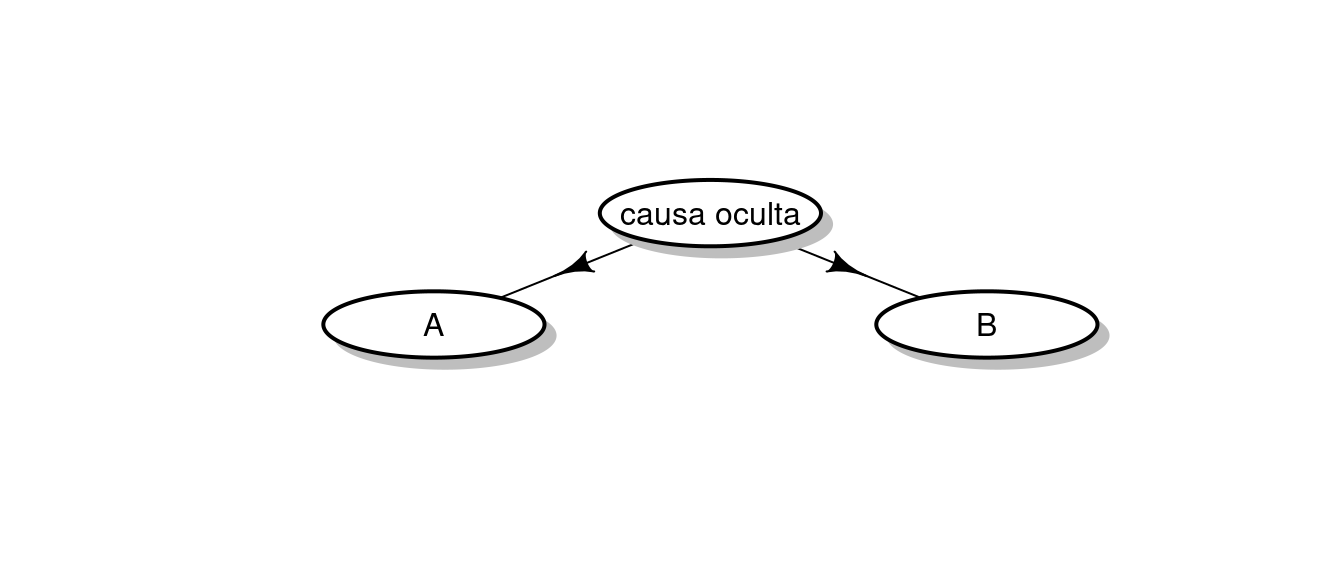
En esos casos también ocurre que \(P(A \; | \; B) \ne P(A)\) porque, de nuevo, conocer B revela información sobre A. El ejemplo clásico que suele citarse es el de que durante muchos años, la industria del tabaco argumentó que podría ser posible que existiese alguna causa biológica que tuviese dos efectos: propensión a la adicción al tabaco y propensión a desarrollar determinados tipos de tumor. Pero cuando uno lee artículos en los que se vincula el nivel de contaminación del aire con el número de hospitalizaciones por determinadas enfermedades respiratorias argumentando que ambos indicadores se mueven en paralelo a lo largo del año, uno siempre puede plantearse si ambas tienen una causa común llamada invierno.
Ni que decir tiene que en situaciones reales las relaciones entre variables pueden ser mucho más complejas y que prácticamente ningún fenómeno, particularmente fuera de los campos de la física o la ingeniería, es monocausal.
5.5 Apéndice: SamIam
SamIam (Automated Reasoning Group at UCLA 2010) es una herramienta para modelar y razonar sobre redes bayesianas desarrollado en la Universidad de California en Los Ángeles (UCLA). Permite representar relaciones de dependencia entre variables aleatorias discretas a través de una interfaz gráfica y, luego, realizar cálculos sobre ellas.
SamIam se puede descargar libremente y los tutoriales en línea ilustran con detalle los dos tipos de operaciones básicas en su manejo:
- Cómo crear variables aleatorias y especificar las probabilidades marginales y condicionales que definen su estructura probabilística.
- Cómo realizar inferencias sobre la red (p.e., marcar un nodo que representa la variable aleatoria que indica el color de una bola extraída de una urna como blanco para ver cómo varían el resto de las probabilidades).
5.6 Bibliografía razonada
Manuales de teoría de probabilidad al uso tales como (Gnedenko 1998) o (Gallier 2014) proporcionan una introducción tal vez más extensa, detallada y formal al asunto tratado en este capítulo.
La discusión sobre la causalidad ha sido extremadamente sobria, hasta el extremo en incurrir en sobresimplificaciones que aquí se quieren enmendar a golpe de bibliografía. Los humanos parecemos programados para preguntarnos por el por qué de las cosas (aunque existen opiniones discrepantes como (Anderson, C. 2008)). La ciencia de datos pretende e intenta comprender el mundo que nos rodea a través de los datos y, sin embargo, el libro argumenta que la causalidad es inasequible tanto para la teoría de la probabilidad como para gran parte de lo que conocemos como estadística. Ocurre que la manera más segura para poder establecer relaciones causales no tiene que ver tanto con el análisis de los datos sino sobre la manera en que estos se recogen. De cómo organizar la recogida de datos para poder descubrir relaciones causales se encarga la disciplina del diseño de experimentos (Design of experiments 2020), que tiene manifestaciones, límites, procedimientos e incluso recibe nombres distintos según el ámbito de aplicación: ingeniería, medicina, sicología, economía, etc. (véase (Sampedro 1983)).
Desafortunadamente, existe también la urgencia por establecer relaciones causales a partir de datos observacionales, es decir, recogidos sin los protocolos que establece el diseño experimental. Esto ocurre, por ejemplo, en epidemiología, cuando se detecta un brote infeccioso y urge identificar los fabricantes y los lotes de comida que puedan haberlo causado (puede consultarse, por ejemplo, (2011 Germany E. coli outbreak 2020)). La falta de datos experimentales —e incluso la imposibilidad práctica misma de obtenerlos— obliga en ocasiones a intentar obtener conclusiones causales a partir de datos observacionales (véase (Gil Bellosta, Carlos J. 2011)). De una manera más formal, los trabajos de Pearl (y, en particular, (Pearl 2009), cuyo último capítulo es una excelente introducción histórica al problema de la causalidad) tratan el mismo problema: la determinación de relaciones causales cuando no se cuenta con datos experimentales.
Aunque, en el fondo, ¿qué consecuencias tiene dar por buena una relación causal que, en el fondo, no existe? El autor está tentado, llegado a este punto, podría hilar anécdotas recopiladas a lo largo de su experiencia laboral, pero en términos de categorías recomienda reflexionar sobre (Goodhart’s law 2020) y (Lucas critique 2020).
Finalmente, existe mucho material publicado sobre el teorema de Bayes y sus aplicaciones, algo sobre lo que se volverá en capítulos posteriores de este libro. Mucha de esta literatura es técnica o semitécnica, aunque cabe mencionar un par de libros ((Mcgrayne 2012) y (Silver 2012)) que no solo tratan la cuestión desde un punto de vista divulgativo e intuitivo sino que, al parecer de muchos y sobre todo en el segundo caso, lo consiguen.
5.7 Ejercicios
Ejercicio 5.3 En una empresa de seguros los clientes son hombres (60%) y mujeres (40%). Tienen coches de color rojo, gris u otros. Para los hombres, el porcentaje de coches grises y de otros colores es igual, pero el de coches rojos es el doble que los anteriores. Para las mujeres, sucede lo mismo, solo que el porcentaje de coches rojos es la mitad que los otros.
La tasa de siniestros (si un cliente tuvo un siniestros en un año dado) es del 10% para hombres y mujeres independientemente del color del coche con las siguientes excepciones:
- Es el doble para los hombres que conducen coches rojos.
- Es la mitad para las mujeres que conducen coches grises.
Dibuja la gráfica que describe las probabilidades anteriores.
Ejercicio 5.4 Construye la tabla de probabilidad conjunta asociada a las variables aleatorias descritas en el ejercicio anterior.
Ejercicio 5.5
- Calcula la probabilidad marginal de los colores de los coches.
- Calcula la probabilidad marginal de colores y siniestralidad (una tabla que contenga la probabilidad de que un coche de un determinado color tenga o no un accidente).
Ejercicio 5.6 Calcula la probabilidad de siniestro según el color del vehículo.
Ejercicio 5.7 De ocurrir un siniestro, calcula la probabilidad de que la afectada sea mujer.
Ejercicio 5.8 Usa SamIam para modelar el problema de la empresa de seguros y úsalo para resolver los ejercicios relacionados con el teorema de Bayes planteados más arriba.
Ejercicio 5.9 Hay tres urnas que contienen, respectivamente, 2, 3 y 5 bolas blancas y 2, 4 y 1 bolas negras. Alguien elige una urna al azar y extrae una bola, que resulta ser blanca. ¿Cuál es la probabilidad de que la urna de la que se ha extraído la bola sea la primera?
Ejercicio 5.10 Recalcula la probabilidad si se extrae una bola más y resulta ser negra.
Ejercicio 5.11 Modela el ejercicio anterior usando SamIan y resuélvelo con él.
Ejercicio 5.12 Prueba que si \(A \perp B\), entonces \(A \perp \bar{B}\) y \(\bar{A} \perp \bar{B}\).
Ejercicio 5.13 Si el saber que Messi está lesionado incrementa las probabilidad de que el Barcelona pierda el próximo partido, ¿qué pasa si se sabe que Messi no está lesionado? En general, si A aumenta la probabilidades de B, ¿qué pasa con \(P(B)\) si se sabe que no ocurre A? ¿Qué tiene que ver lo anterior con la descomposición (pruébala) \(P(B) = P(B \; | \; A) P(A) + P(B \; | \; \bar{A}) P(\bar{A})\)?
Ejercicio 5.14 Calcula la probabilidad de obtener 3 caras en 4 lanzamientos de monedas.
Ejercicio 5.15
- ¿Cuál es la probabilidad de sacar un 2 o un 6 tirando un dado? (Usa los axiomas de probabilidad)
- ¿Cuál es la probabilidad de sumar 7 puntos en dos tiradas de dados?
- ¿Cuál es la probabilidad de no sacar un 1 tirando un dado?
- ¿Cuál es la probabilidad de no sacar ningún 1 después de tirar n dados? (Usa la independencia)
Ejercicio 5.16 ¿Qué es más probable, sacar un as tirando cuatro dados (una vez), o sacar dos ases en alguna de 24 tiradas de dos dados? (Es el problema del caballero de Méré)
Ejercicio 5.17 Demostrar que \(P(A\;|\; B, A \cup B) \le P(A ;|\; A \cup B)\), desigualdad conocida como la paradoja de Berkson.
Referencias
2011 Germany E. coli outbreak. 2020. “2011 Germany E. Coli O104:H4 Outbreak — Wikipedia, the Free Encyclopedia.” https://en.wikipedia.org/wiki/2011_Germany_E._coli_O104:H4_outbreak.
Anderson, C. 2008. “The End of Theory: The Data Deluge Makes the Scientific Method Obsolete.” https://www.wired.com/2008/06/pb-theory/.
Automated Reasoning Group at UCLA. 2010. “Samian: Sensitivity Analysis, Modelling, Inference and More.” http://reasoning.cs.ucla.edu/samiam/.
Design of experiments. 2020. “Design of Experiments — Wikipedia, the Free Encyclopedia.” https://en.wikipedia.org/wiki/Design_of_experiments.
Gallier, J. 2014. An Introduction to Discrete Probability. http://www.cis.upenn.edu/~jean/proba.pdf.
Gil Bellosta, Carlos J. 2011. “Causalidad O Asociación: Indicios de La Primera.” https://www.datanalytics.com/2011/04/20/causalidad-o-asociacion-indicios-de-la-primera/.
Gnedenko, B. V. 1998. Theory of Probability. Taylor & Francis.
Goodhart’s law. 2020. “Goodhart’s Law — Wikipedia, the Free Encyclopedia.” https://en.wikipedia.org/wiki/Goodhart%27s_law.
Lucas critique. 2020. “Lucas Critique — Wikipedia, the Free Encyclopedia.” https://en.wikipedia.org/wiki/Lucas_critique.
Mcgrayne, S. 2012. The Theory That Would Not Die: How Bayes’ Rule Cracked the Enigma Code, Hunted down Russian Submarines, and Emerged Triumphant from Two Centuries of Controversy.
Pearl, J. 2009. Causality: Models, Reasoning and Inference. 2nd ed. USA: Cambridge University Press.
Sampedro, J. L. 1983. “El Reloj, El Gato Y Madagascar.” Revista de Estudios Andaluces. https://doi.org/10.12795/rea.1983.i01.09.
Silver, N. 2012. The Signal and the Noise.
Esto no es rigurosamente cierto: véase la bibliografía razonada del capítulo para más información.↩︎