Capítulo 3 Probabilidades condicionales e independencia

En este capítulo, fundamentalmente, se presentan los conceptos de probabilidad condicional y el de independencia. Ambos se van a tratar como formalizaciones de conceptos comunes en el uso cotidiano de la probabilidad.

Ambos tienen aplicaciones directas en el ámbito de la ciencia de datos, algunas de las cuales se mencionarán en este capítulo. La independencia, además, servirá en capítulos posteriores para fundamentar otros resultados más profundos y útiles de la teoría de la probabilidad.

3.1 Probabilidades condicionales

El concepto de probabilidad condicional está presente en el habla cotidiana. Son comunes, por ejemplo, expresiones del tipo:

Cuando llueve, la probabilidad de que se produzcan atascos es del 40%.

Si \(A\) es el evento atascos, la expresión anterior no significa que \(P(A) = .4\): \(A\) incluye también el evento atasco en ausencia de lluvia. Si \(B\) es el evento lluvia, la manera en que se representa la expresión anterior es

\[P(A \; | \; B ) = .4,\]

que se lee así: la probabilidad condicional de \(A\) dado \(B\) es del 40%.

Supóngase ahora que de cada 100 días, 10 llueve. Es decir, que \(P(B) = .1\). Entonces, de cada 100 días, 4 lloverá y habrá atasco. Es decir, \(P(A \cap B) = 0.04\). En general,

\[P(A \cap B) = P(A | B) \times P(B)\]

o, como se suele ver escrito por todas partes,

\[P(A | B) = \frac{P(A \cap B)}{P(B)}.\]

Ejercicio 3.1 Supóngase que \(P(A) = .2\) y \(P(B) = .5\). Entonces, ¿cuáles de las siguientes afirmaciones son necesariamente ciertas?

• \(P(A | B) = .1\)
• \(P(A | B) \le .4\)
• \(P(A | B) > 0\)

¿Puedes ilustrar tu razonamiento con ejemplos concretos y cotidianos?

El concepto de la probabilidad condicional aparece en muchos contextos, frecuentemente con denominaciones específicas. Por ejemplo, en epidemiología se distingue entre la tasa de mortalidad (o la probabilidad de morir a causa de una determinada enfermedad), que podríamos representar como \(P(M)\) y la tasa de letalidad, \(P(M\;|\;C)\), que es la probabilidad de morir condicionada a haber contraído la enfermedad. También se habla de tasa de paro (la probabilidad de estar desempleado) y, p.e., tasa de paro femenina, o la probabilidad de que una mujer se encuentre desempleada, que es la probabilidad de que una persona esté desempleada condicionada a que dicha persona es mujer (o \(P(D\;|\;M)\)).

Hablar de probabilidades condicionales viene a ser equivalente a cambiar (o estrechar) el marco de referencia, el evento total. De hecho, por lo anterior,

\[P(B | B) = \frac{P(B \cap B)}{P(B)} = \frac{P(B)}{P(B)} = 1.\]

Al condicionar por \(B\), por lo tanto, se está reemplazando el conjunto total, \(\Omega\), por \(B\). En el ejemplo concreto con el que se inicia esta sección, eso significa que ya no se tienen en cuenta todas las condiciones meteorológicas posibles sino solamente aquellas en que llueve.

Ni que decir tiene que también es posible condicionar usando eventos definidos por variables aleatorias. En tal caso, por abreviar, se usa la notación

\[P(A | X = a)\]

para representar la probabilidad de \(A\) condicionada por evento en que la variable aleatoria \(X\) toma el valor \(a\). También se usan otras expresiones análogas cuyo significado se entenderá sin problemas en su contexto.

3.1.1 Probabilidades condicionales y ciencia de datos

Las probabilidades condicionales constituyen, podría decirse, el núcleo de la ciencia de datos. En un banco, por ejemplo, \(P(H)\) podría representar la probabilidad de impago de una hipoteca y mostrarse, tal vez gráficamente, en un cuadro de mando tras calcularse mediante una consulta a la base de datos. También podrían mostrarse las probabilidades condicionales \(P(H \;|\;\text{provincia})\), posiblemente sobre un mapa. Porque, efectivamente, existe una relación conceptual entre las probabilidades condicionales y las operaciones basadas en la expresión group by de SQL.

Trascendiendo ese mundo de indicadores simples, un modelo de los usados en ciencia de datos no es otra cosa que una estimación más o menos problemática de \(P(H \;|\; X_1, \dots, X_n)\), la probabilidad de un impago (en este caso) dadas —o condicionadas a— una serie de eventos \(X_1, \dots, X_n\) que tratan de describir las circunstancias de un cliente concreto y que podrían incluir no solo su provincia, sino también su edad, sus ingresos, su historial crediticio, etc.

3.1.2 Aspectos epistemológicos de las probabilidades condicionales

Esa sección puede omitirse en una primera lectura. Aunque puede servirle al lector para fundamentar su intuición sobre las probabilidades condicionales.

Lo siguiente es cierto: si \(x = 5\) e \(y = 7\), entonces \(x < y\). Sin embargo, la proposición \(x < y\) no es necesariamente cierta: solo lo es si ha quedado claro que \(x = 5\) e \(y = 7\). Incluso podría decirse que la expresión \(x < y\) por sí sola no tiene sentido.

Esa es la línea de razonamiento que han seguido muchos (véase, por ejemplo, (Keynes 1921)) para argumentar que expresiones del tipo \(P(A) = .3\) no tienen sentido: no existe tal cosa como \(P(A)\) sino, tal vez, \(P(A | H)\) donde \(H\) es un evento que recoge las hipótesis bajo las cuales se está examinando la probabilidad de \(A\).

Esta necesidad es particularmente acuciante en el ámbito de las probabilidades subjetivas, aquellas que un sujeto —valga la redundancia— asigna a eventos condicionado por la información que se dispone acerca de ellos en un momento dado.

La salvedad es relevante en tanto que nos advierte sobre la necesidad de explicitar muy claramente el marco concreto en el que hay que entender juicios del tipo \(P(A) = .3\). No lo es tanto, sin embargo, en cuanto a la advertencia de que toda probabilidad es condicional. El formalismo de Kolmogorov, que define un espacio probabilístico en términos de la terna \((\Omega, B, P)\), permite establecer el marco en el que \(P(A) = .3\) tiene un sentido unívoco sin recurrir a las probabilidades condicionales.

3.2 Probabilidades conjuntas y marginales

En esta sección se introducen dos conceptos adicionales muy útiles en estadística y en ciencia de datos: los de probabilidades conjuntas y marginales. No siempre se hace referencia a ellos por estos nombres, pero es fácil identificarlos en operaciones habituales en la práctica.

A lo largo de esta sección se utilizará a modo de ejemplo el siguiente modelo probabilístico:

• En un determinado lugar, el 10% de los días llueve y el 90% luce el sol.
• Cuando llueve, la probabilidad de que se produzcan atascos es del 40%.
• Cuando no llueve, la probabilidad de que se produzcan atascos es del 10%.

Un modelo probabilístico es una descripción teórica de un fenómeno aleatorio. En un modelo probabilístico intervienen típicamente ciertas variables aleatorias que interactúan de una determinada forma.

El modelo se puede representar gráficamente así:

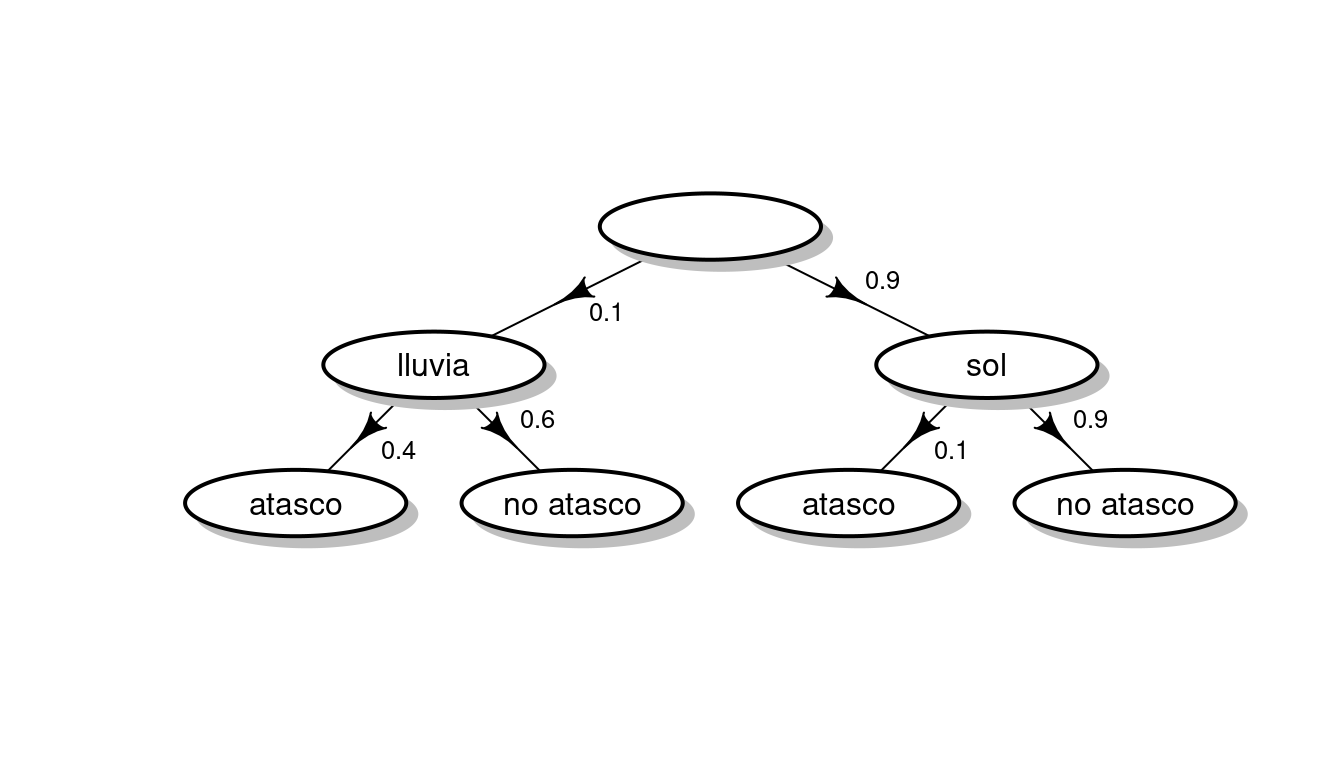
Gráficas como la anterior abundan en la literatura dedicada a construir representaciones relacionadas con conceptos probabilísticos que tienen como objetivo hacerlas más fáciles de interpretar y, de paso, tratar de evitar determinados errores en los que los humanos incurrimos con excesiva frecuencia (véase (Hoffrage et al. 2002)).

Expresiones del tipo el 10% de los días llueve reciben el nombre de probabilidades marginales (por un motivo que luego quedará claro).

La probabilidad de que un día llueva y no haya atasco es \(0.06 = 0.1 \times 0.6\): el 10% de los días llueve y de ellos, el 60% no hay atascos. Análogamente, se puede calcular el resto de las combinaciones posibles y tabularlas así:

tiempo	atasco	probabilidad
sol	sí	0.09
sol	no	0.81
lluvia	sí	0.04
lluvia	no	0.06

Esta tabla representa la llamada probabilidad conjunta (de las variables aleatorias: \(T\), o tiempo, y \(A\), o atasco). Nótese cómo la suma de las probabilidades es 1. Se ha construido a partir de las probabilidades marginales (del tiempo) y condicionales (de los atascos condicionados por el tiempo).

Ejercicio 3.2 La tabla anterior representa las probabilidades conjuntas de dos variables aleatorias que pueden asumir dos valores cada una de ellas y tiene 4 filas. ¿Cuántas filas tendría si se computasen las probabilidades conjuntas de tres variables aleatorias de ese tipo? ¿Y si las variables aleatorias pudiesen asumir tres valores en lugar de solo dos? ¿Cuál es la regla general?

La tabla de probabilidades conjuntas también puede representarse de la forma equivalente

P(T,A)	atasco	no atasco
lluvia	0.04	0.06
sol	0.09	0.81

Frecuentemente, en lugar de usar \(P(A \cap B)\), por comodidad y a pesar de la ambigüedad que introduce la notación, se escribe \(P(A, B)\). En todo lo que sigue se usará una u otra notación indistintamente.

En ella, si se suman filas y columnas, se obtienen las probabilidades marginales:

P(T,A)	atasco	no atasco	P(T)
lluvia	0.04	0.06	0.1
sol	0.09	0.81	0.9
P(A)	0.13	0.87	1

Nótese cómo las probabilidades marginales de \(T\) eran dato: estaban en la descripción del modelo probabilístico original. Sin embargo, las probabilidades marginales de la otra variable, \(A\), eran desconocidas y han sido obtenidas mediante los cálculos anteriores. Ahora sabemos, pues, que la probabilidad de atasco independientemente de las condiciones meteorológicas es del 13%.

Ejercicio 3.3 Examinando la tabla anterior, de saberse que hay un atasco, ¿cuál sería la probabilidad de que estuviese lloviendo? ¿Y la de que haga sol si no hay atasco?

En el modelo probabilístico de esta sección solo intervienen dos variables aleatorias, \(T\) y \(A\). Otros modelos probabilísticos pueden requerir más variables y su probabilidad conjunta se representaría por medio de un (hiper)cubo de números (que seguirían sumando 1). En tales casos, las probabilidades marginales corresponderían a las sumas a lo largo de las distintas proyecciones. Por ejemplo, de tenerse las variables \(A\), \(B\) y \(C\), la probabilidad marginal \(P(A,B)\) se calcular a partir de la conjunta así:

\[P(A,B) = \sum_i P(A,B, C = c_i).\]

La operación anterior recibe el nombre de marginalización.

Recuérdese cómo los valores de la tabla de probabilidades conjuntas, \(P(T,A)\), se han calculado más arriba así:

\[P(T,A) = P(A \; | \; T) P(T).\]

Despejando, se obtiene la relación conocida

\[ P(A \; | \; T) = \frac{P(T,A)}{P(T)} = \frac{P(T \cap A)}{P(T)}\]

que se usa a menudo como definición de la probabilidad condicional. Lo que dice la fórmula anterior es que la probabilidad \(P(A \; | \; \text{lluvia})\) se construye tomando la columna correspondiente de la tabla de probabilidades conjuntas y, como sus valores no suman la unidad, normalizando por su total, que es precisamente \(P(\text{lluvia})\).

3.2.1 Teorema de la probabilidad total

Para finalizar esta sección, merece la pena repasar cómo se ha calculado la probabilidad marginal de, por ejemplo, el atasco, \(A\). Se ha hecho en las tablas anteriores sumando verticalmente

\[P(A) = P(A, \text{lluvia}) + P(A, \text{sol}).\]

Pero, desarrollando la expresión anterior en términos de las probabilidades condicionales conocidas, se obtiene la expresión

\[P(A) = P(A \;|\; \text{lluvia}) P(\text{lluvia}) + P(A \;|\; \text{sol}) P(\text{sol}).\]

En general, si nos interesa calcular la probabilidad de un evento \(A\) y somos capaces de encontrar conjuntos disjuntos \(B_i\) tales que tanto \(P(B_i)\) como \(P(A \;|\; B_i)\) son conocidos, entonces podemos calcular

\[P(A) = \sum_i P(A \;|\; B_i) P(B_i),\]

expresión es conocida con el desafortunado nombre de teorema de la probabilidad total; divide y vencerás sería más adecuado.

Dado que \(\sum_i P(B_i) = 1\), \(P(A)\) es lo que se llama una combinación convexa de las probabilidades condicionales \(P(A \;|\; B_i)\).

Más adelante en el libro se discutirá el problema de estimar las probabilidades de eventos. El teorema de la probabilidad total es una herramienta que permite estimar la probabilidad de eventos complejos. De hecho, conceptos relacionados con este teorema son recurrentes en libros dedicados en exclusiva al tema de estimación de probabilidades y a la realización de predicciones, como (Tetlock and Gardner 2015). En ese libro se describe la tarea de unos equipos que compiten estimando la probabilidad de eventos de significancia estratégica (p.e., ¿habrá un cambio de régimen en Corea del Norte en los próximos cinco años?). Una de las herramientas que usan estos pronosticadores es, precisamente, la de descomponer esos eventos en otros más simples (p.e., se reactivará la guerra con el vecino del sur; fallecerá el líder; el ejército protagonizará un golpe de estado; etc.), estimar sus probabilidades marginales y condicionales y recomponer usando el teorema de la probabilidad total la del evento de interés.

3.3 Independencia

La relación de independencia es tal vez la más simple (entre las no triviales, como por ejemplo, ser iguales o complementarios) que puede existir entre eventos. Dos eventos \(A\) y \(B\) son independientes —y se suele escribir que \(A \perp B\)— cuando

\[P(A \cap B) = P(A) \times P(B).\]

Si se reescribe la definición anterior en términos de las probabilidades condicionales, queda de la forma

\[P(A | B) = P(A),\]

que es mucho más intuitiva: da mucho mejor a entender que el conocimiento de B no afecta para nada a la probabilidad de \(A\). Siguiendo con el ejemplo futbolístico, si \(A\) es el evento relacionado con la victoria en liga del equipo local y \(B\) es algún tipo de evento en las lunas de Saturno, es plausible que \(P(A | B) = P(B)\).

Las condiciones \(P(A,B) = P(A)P(B)\) o \(P(A|B) = P(A)\), que pueden usarse indistintamente como definiciones de independencia de eventos, no son realmente las que uno usa al enfrentarse a problemas reales. Frecuentemente no queda otra que remitirse al concepto intuitivo y cotidiano de independencia.

Por extensión, se dice que dos variables aleatorias \(X\) e \(Y\) son independientes cuando lo son los eventos que generan, es decir, cuando

\[P(X = a | Y = b) = P(X = a)\]

para todos los valores \(a\) y \(b\).

En el modelo probabilístico discutido más arriba, el estado del tráfico dependía del tiempo. Había una correlación —y podría argumentarse que una relación causal— entre ambas variables aleatorias. Sin embargo, en muchas circunstancias se opera con variables aleatorias que se pueden considerar independientes. Un ejemplo clásico —el ejemplo clásico— es el de los lanzamientos sucesivos de una moneda. Si se tira una moneda al aire, se puede suponer que \(P(H) = P(T) = 1/2\). Pero, ¿qué ocurre si se lanza al aire dos veces? Gráficamente,

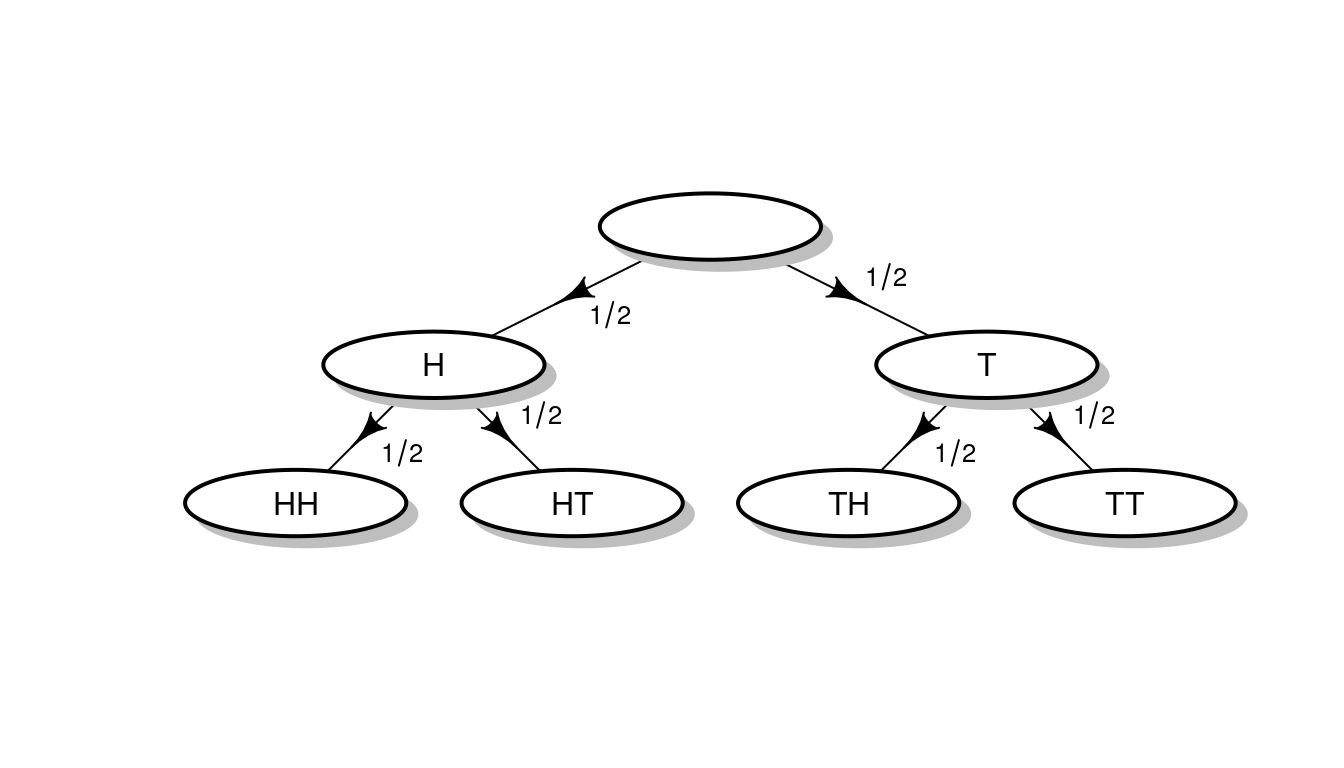
En el ejemplo original, como el estado del tiempo afecta al del tráfico,

\[P(\text{atasco} \; | \; \text{lluvia}) \neq P(\text{atasco} \; | \; \text{sol})\]

Pero en los lanzamientos de monedas,

\[P(H_2 \; | \; H_1) = P(H_2 \; | \; T_1)\]

y

\[P(T_2 \; | \; H_1) = P(T_2 \; | \; T_1).\]

Es decir, el resultado de la segunda tirada no está afectado por el de la primera y, de hecho,

\[P(H_2 \; | \; H_1) = P(H_2 \; | \; T_1) = P(H) = 1/2.\]

Cuando \(A\) y \(B\) son independientes, su probabilidad conjunta, dado que \(P(A,B) = P(A\; |\; B)P(B) = P(A)P(B)\), es así de simple:

P(A,B)	b0	b1	P(A)
a0	p1 * p3	p1 * p4	p1
a1	p2 * p3	p2 * p4	p2
P(B)	p3	p4	1

A partir de las probabilidades conjuntas pueden construirse las marginales. Pero la reconstrucción de las condicionales a partir de las marginales es imposible en general (véase la nota al respecto en las sección de la bibliografía razonada). Sin embargo, en el caso trivial en que las variables aleatorias son independientes, la reconstrucción de las probabilidades condicionales es tan simple como se ha indicado en el párrafo precedente.

3.3.1 Independencia y ciencia de datos

Podría decirse que los eventos independientes interactúan todos entre sí de la misma manera, cualquiera que sea su naturaleza. Eso permite probar muchos resultados interesantes. En capítulos sucesivos se mostrarán algunos de los más importantes.

Sin embargo, desde el punto de vista de la práctica de la ciencia de datos, la independencia es una propiedad más problemática: no solo es una propiedad cuasiquimérica —en el sentido de que realmente es difícil observar variables que sean estrictamente independientes—, sino que ni siquiera es deseable: para poder decir algo respecto a la probabilidad de un evento \(A\) a partir de otros eventos conocidos \(B_1, \dots, B_n\), interesa precisamente que los \(B_i\) no sean independientes de \(A\). De otra manera, si estamos interesados en explicar una variable aleatoria \(Y\) construyendo modelos basados en otras variables \(X_1, \dots, X_n\) interesa que \(Y\) no sea independiente de ninguna de las \(X_i\).

La ciencia de datos es posible gracias a una especie de discontinuidad causal (Bueno 2010). Si todos los fenómenos fuesen mutuamente interdependientes, no solo la ciencia de datos sino el conocimiento mismo sería imposible: para modelar cualquiera de ellos haría falta tener en cuenta todos los demás (incluido el proverbial aleteo de las mariposas del trópico). Lo mismo pasaría si nada guardase relación con nada: cada fenómeno sería una manifestación de un azar no sujeto a pauta alguna. Pero, generalmente, si interesa \(A\), se puede identificar un número razonable de fenómenos \(B_1, \dots, B_n\) relacionados con \(A\) que permiten acotar su comportamiento y, en la práctica, crear modelos.

Dos conceptos adicionales relacionados con la discusión precedente y que son de la máxima relevancia para la ciencia de datos son:

• El llamado factor crud (Orben and Lakens 2020) que hace referencia al hecho empírico de que en la práctica, es casi imposible encontrar variables aleatorias independientes. Dicho de otra manera, entre dos variables aleatorias reales es muy probable que exista algún tipo de relación.
• El llamado problema de la piraña (Tosh et al. 2021), estudia el número máximo de variables aleatorias que pueden llegar a tener un efecto importante en una de interés: es imposible que existan muchas variables aleatorias impactando significativamente en otra sin que haya algún tipo de solapamiento entre las primeras.

Finalmente, existe otro modo en que consideraciones sobre la independencia de variables juegan un papel en la ciencia de datos. Tiene que ver con la relación entre las distintas observaciones \(y_i\). Frecuentemente, son independientes entre sí. Sin embargo, en muchos problemas interesantes no lo son. Por ejemplo:

• Si las \(y_i\) son observaciones ordenadas en el tiempo (p.e., temperaturas horarias).
• Si las \(y_i\) se refieren a ubicaciones (puesto que se correlacionan con otras \(y_j\) próximas).
• Si bloques de \(y_i\) se refieren a un mismo cliente, paciente o sujeto.

En esos casos, ignorar las relaciones de dependencia y asumir de facto la independencia de las observaciones conduce a modelos menos eficaces. Por eso existen modelos específicos para series temporales, modelos espaciales o los llamados modelos de medidas repetidas que se pueden aplicar, respectivamente, a los casos enumerados arriba. El quid de la cuestión reside en que asumir independencia cuando no la hay equivale a descartar información potencialmente útil.

3.3.2 Regla de la cadena e independencia condicional

En el modelo probabilístico considerado en este capítulo se ha estudiado la interacción de dos variables aleatorias, \(T\) y \(A\), y se han obtenido las probabilidades conjuntas factorizando de la siguiente manera:

\[P(T,A) = P(A \; | \; T) P(T)\]

Más en general, si el modelo hubiese involucrado las cuatro variables aleatorias \(A_1\), \(A_2\), \(A_3\) y \(A_4\), se habría cumplido la llamada regla de la cadena:

\[P(A_1, A_2, A_3, A_4) = P(A_4 \; | \; A_1, A_2, A_3) P(A_3 \; | \; A_1, A_2) P(A_2 \; | \; A_1)P(A_1)\]

Esto se puede demostrar dibujando el gráfico correspondiente: se comienza con \(A_1\), se hace depender \(A_2\) de \(A_1\) y así sucesivamente. Obviamente, la factorización tiene sentido cuando se conocen las probabilidades condicionales implicadas.

Ahora, de ser mutuamente independientes, la expresión anterior se reduciría a

\[P(A_1, A_2, A_3, A_4) = P(A_1) P(A_2) P(A_3)P(A_4).\]

Así ocurre al lanzar de monedas, donde, de hecho, se tiene, por ejemplo, que

\[P(HHTHT) = \frac{1}{2^5}.\]

La independencia mutua de variables aleatorias es una propiedad más fuerte que la de ser independientes dos a dos: exige que \(P(A_1 \cap \dots \cap A_n) = \prod P(A_i)\). De otra manera, la relación anterior no tendría que cumplirse necesariamente. Véase el siguiente ejercicio.

Ejercicio 3.4 Describe tres eventos cotidianos \(A\), \(B\) y \(C\) tales que \(A \perp B\), \(A \perp C\), pero que no se cumpla \(A \perp B \cap C\). Pista: puedes pensar en un evento \(A\) tal que \(B\) pueda tener un impacto positivo o negativo sobre su probabilidad de ocurrencia pero nulo en promedio y que ocurra lo mismo entre \(A\) y \(C\) pero que, sin embargo, \(A\) se vea afectado (p.e., negativamente) cuando ocurren simultáneamente \(B\) y \(C\).

El ejercicio anterior está estrechamente relacionado con un concepto fundamental de la ciencia de datos que es el de las interacciones entre variables: el efecto combinado de dos puede ser mayor (o menor) que el agregado de ambas por separado.

Hay problemas en probabilidad (y en ciencia de datos) que conllevan el estudio de expresiones del tipo

\[P(A_1, A_2, \dots, A_n).\]

que, como se ha indicado antes, en el caso en el que los eventos involucrados son independientes, pueden factorizarse trivialmente:

\[P(A_1, A_2, \dots, A_n) = \prod_i P(A_i).\]

A medio camino entre el caso de la dependencia entre todas las variables y el caso de las variables aleatorias independientes existe una gran variedad de modelos caracterizados por la estructura de las relaciones de independencia entre las variables aleatorias involucradas.

Por ejemplo, existe una serie de modelos que reciben diversos nombres (modelos gráficos, redes bayesianas, etc.) que permiten modelar explícitamente las relaciones de independencia, de haberlas, y la forma concreta de la relación de dependencia en el resto de los casos. Se volverá a ellas brevemente en un capítulo posterior.

Existe otro tipo de casos en los que se puede suponer, por ejemplo, que \(A_4\) no depende de \(A_1\) y \(A_2\), por lo que la expresión potencialmente compleja \(P(A_4|A_1, A_2, A_3)\) se reduce a la más manejable \(P(A_4|A_3)\). Sucede así, por ejemplo, con los llamados paseos aleatorios \(X_t\): una partícula, que en \(t = 0\) está en la posición \(0\) se mueve aleatoriamente cada segundo dando saltos equiprobables de tamaño \(-1\), \(0\) o \(1\).

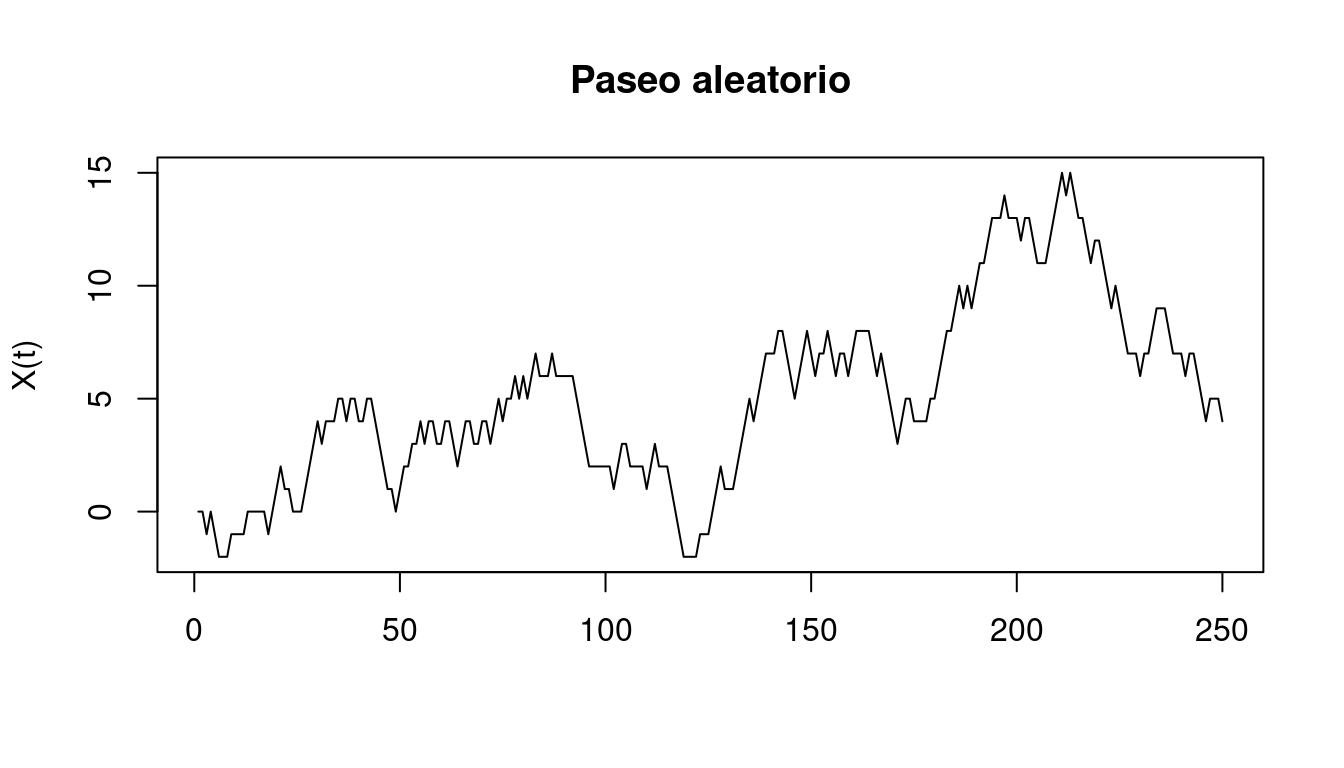
Entonces, \(X_T\) depende de \(X_t\) si \(t < T\), pero, conocido \(X_{T-1}\), \(X_T\) no depende de por dónde haya pasado previamente. Es decir, \(X_T\) no es independiente de \(X_t\), pero ambas variables aleatorias son condicionalmente independientes dado \(X_{T-1}\). La independencia condicional se representa así:

\[X_T \perp X_t \; | \; X_{T-1} \;\; \text{si} \; t < T-1.\]

En tales casos, la función de probabilidad conjunta puede factorizarse de la siguiente manera:

\[P(X_0, X_1, \dots, X_T) = P(X_0) \prod_{i = 1}^T P(X_i \; | \; X_{i-1}).\] Es una expresión un poco más compleja que la correspondiente a eventos independientes pero mucho más simple que la que se deduce de la regla de la cadena general. Precisamente porque se explotan las relaciones de independencia condicional.

Ejemplos como los de las caminatas aleatorias son campo minado para las probabilidades subjetivas de determinado tipo de sujetos siempre prestos a identificar relaciones entre \(X_T\) y secuencias de \(X_t\) previos tendencias o patrones de cualquier otro tipo. Ese impulso más o menos patológico recibe el nombre de apofenia.

El anterior es un ejemplo simple de las cadenas de Markov, que son secuencias de variables aleatorias en las que cada una de ellas es condicionalmente independiente de todas las que la preceden no inmediatamente condicionalmente en, precisamente, su predecesora inmediata.

El concepto de independencia condicional no es una mera construcción matemática sino un concepto usado implícitamente en muchas aplicaciones de la ciencia de datos. Por ejemplo, que un jubilado de Galicia y una señora de Cuenca hayan comprado un determinado producto, a pesar de la distancia, a pesar de no conocerse mutuamente, no tienen por qué ser eventos independientes: que el producto esté sujeto a una misma oferta, que ambos hayan visto el mismo anuncio,… Si el producto es, por ejemplo, turrón, el que lo haya comprado \(A\) aumenta las probabilidades de que lo haya comprado \(B\) porque, casi seguro, esos eventos están sucediendo en época de navidad. Sin embargo, al crear un modelo estamos aspirando a recoger sobre los sujetos involucrados una serie de variables tal que, a la vista de ellas, los comportamiento de los sujetos sean independientes. Es decir, estamos tratando de forzar relaciones de independencia condicional.

3.4 Bibliografía razonada

Manuales de teoría de probabilidad al uso tales como (Gnedenko 1998) o (Gallier 2014) proporcionan una introducción tal vez más extensa, detallada y formal al asunto tratado en este capítulo. Otra introducción alternativa a los mismos conceptos que abre la puerta al estudio de los modelos gráficos es (Koller and Friedman 2009).

Como se ha indicado más arriba, el formalismo de Kolmogorov hace de alguna manera innecesario explicitar el marco de referencia dentro del cual entendemos expresiones del tipo \(P(A) = .5\). Sin embargo, en el clásico (Keynes 1921) o en el mucho más moderno y muy recomendable (Jaynes 2003), que argumentan desde posiciones distintas, se pueden encontrar argumentos acerca la necesidad de contextualizarlas a través de probabilidades condicionales explícitas. Alguien puede considerar que esta es una disquisición impráctica, pero conviene recordar aquel suceso, ocurrido hace unos años, en el que una votación vinculante entre varios cientos de delegados de cierto partido político español acabó en empate. Hubo muchos análisis proporcionando cálculos de \(P(E)\), todos distintos. Pero, ¿por qué puede ser una \(P(E)\), una magnitud objetiva, diferente? Lo era porque cada analista \(i\) estaba calculando \(P(E | H_i)\) con una \(H_i\) implícita distinta.

3.5 Ejercicios

Ejercicio 3.5 En una empresa de seguros los clientes son hombres (60%) y mujeres (40%). Tienen coches de color rojo, gris u otros. Para los hombres, el porcentaje de coches grises y de otros colores es igual, pero el de coches rojos es el doble que los anteriores. Para las mujeres, sucede lo mismo, solo que el porcentaje de coches rojos es la mitad que los otros.

La tasa de siniestros (si un cliente tuvo un siniestros en un año dado) es del 10% para hombres y mujeres independientemente del color del coche con las siguientes excepciones:

• Es el doble para los hombres que conducen coches rojos.
• Es la mitad para las mujeres que conducen coches grises.

Dibuja la gráfica que describe las probabilidades anteriores.

Ejercicio 3.6 Construye la tabla de probabilidad conjunta asociada a las variables aleatorias descritas en el ejercicio anterior.

Ejercicio 3.7

• Calcula la probabilidad marginal de los colores de los coches.
• Calcula la probabilidad marginal de colores y siniestralidad (una tabla que contenga la probabilidad de que un coche de un determinado color tenga o no un accidente).

Ejercicio 3.8 Calcula la probabilidad de siniestro según el color del vehículo.

Ejercicio 3.9 De ocurrir un siniestro, calcula la probabilidad de que la afectada sea mujer.

Ejercicio 3.10 Usa SamIam para modelar el problema de la empresa de seguros y úsalo para resolver los ejercicios relacionados con el teorema de Bayes planteados más arriba.

Ejercicio 3.11 Hay tres urnas que contienen, respectivamente, 2, 3 y 5 bolas blancas y 2, 4 y 1 bolas negras. Alguien elige una urna al azar y extrae una bola, que resulta ser blanca. ¿Cuál es la probabilidad de que la urna de la que se ha extraído la bola sea la primera?

Ejercicio 3.12 Recalcula la probabilidad si se extrae una bola más y resulta ser negra.

Ejercicio 3.13 Modela el ejercicio anterior usando SamIan y resuélvelo con él.

Ejercicio 3.14 Prueba que si \(A \perp B\), entonces \(A \perp \bar{B}\) y \(\bar{A} \perp \bar{B}\).

Ejercicio 3.15 Si el saber que Messi está lesionado incrementa las probabilidad de que el Barcelona pierda el próximo partido, ¿qué pasa si se sabe que Messi no está lesionado? En general, si A aumenta la probabilidades de B, ¿qué pasa con \(P(B)\) si se sabe que no ocurre A? ¿Qué tiene que ver lo anterior con la descomposición \(P(B) = P(B \; | \; A) P(A) + P(B \; | \; \bar{A}) P(\bar{A})\)?

Ejercicio 3.16 Calcula la probabilidad de obtener 3 caras en 4 lanzamientos de monedas.

Ejercicio 3.17

• ¿Cuál es la probabilidad de sacar un 2 o un 6 tirando un dado? (Usa los axiomas de probabilidad)
• ¿Cuál es la probabilidad de sumar 7 puntos en dos tiradas de dados?
• ¿Cuál es la probabilidad de no sacar un 1 tirando un dado?
• ¿Cuál es la probabilidad de no sacar ningún 1 después de tirar n dados? (Usa la independencia)

Ejercicio 3.18 ¿Qué es más probable, sacar un as tirando cuatro dados (una vez), o sacar dos ases en alguna de 24 tiradas de dos dados? (Es el problema del caballero de Méré)

Ejercicio 3.19 Demostrar que \(P(A\;|\; B, A \cup B) \le P(A ;|\; A \cup B)\), desigualdad conocida como la paradoja de Berkson.

Referencias

Bueno, G. 2010. “Symploké.” https://www.youtube.com/watch?v=fML2Ysy6l6s.

Gallier, J. 2014. An Introduction to Discrete Probability. http://www.cis.upenn.edu/~jean/proba.pdf.

Gnedenko, B. V. 1998. Theory of Probability. Taylor & Francis.

Hoffrage, Ulrich, Gerd Gigerenzer, Stefan Krauss, and Laura Martignon. 2002. “Representation Facilitates Reasoning: What Natural Frequencies Are and What They Are Not.” Cognition 84 (August): 343–52. https://doi.org/10.1016/S0010-0277(02)00050-1.

Jaynes, E. T. 2003. Probability Theory: The Logic of Science. Cambridge: Cambridge University Press.

Keynes, John Maynard. 1921. A Treatise on Probability. Macmillan & Co.

Koller, D., and N. Friedman. 2009. Probabilistic Graphical Models: Principles and Techniques. Adaptive Computation and Machine Learning. MIT Press. https://books.google.co.in/books?id=7dzpHCHzNQ4C.

Orben, Amy, and Daniël Lakens. 2020. “Crud (Re)Defined.” Advances in Methods and Practices in Psychological Science 3 (2): 238–47. https://doi.org/10.1177/2515245920917961.

Tetlock, Philip E., and Dan Gardner. 2015. Superforecasting: The Art and Science of Prediction. Crown Publishing Group.

Tosh, Christopher, Philip Greengard, Ben Goodrich, Andrew Gelman, Aki Vehtari, and Daniel Hsu. 2021. “The Piranha Problem: Large Effects Swimming in a Small Pond.” https://doi.org/10.48550/ARXIV.2105.13445.