Capítulo 4 Muestras
Dos tipos de fenómenos aleatorios. Con ejemplos:
- Ese ruido, ¿será un oso hambriento?
- Tiradas de dados, juegos de azar repetidos, etc.
Ambos tienen acomodo en el formalismo discutido previamente, pero volvemos a las muestras (gracias a lo que hemos aprendido hasta la fecha).
TODO: intro
Sobre todo, variables aleatorias discretas. Podrían ser no numéricas, pero…
Justificar cómo ha habido que retrasar material trivial hasta poder establecerlo fehacientemente.
El objetivo de esta sección es buscar regularidad en el azar. Poner ejemplos:
- Tiradas de monedas.
- dispersión de las alturas de la gente
- ¿algún ejemplo de varianza constante? Con alguna Poisson?
Estas características nos permiten caracterizar el azar y caracterizar las distribuciones.
¿Que estoy usando una aproximación frecuentista? Por lo de las muestras, etc.
4.1 Concepto histórico de muestra
Aunque la adaptación a la incertidumbre —y la necesidad de tomar decisiones razonablemente buenas bajo incertidumbre— sea una condición para la misma existencia de la vida, es sabido que el estudio de la probabilidad tuvo su origen en el análisis de otro tipo de fenómenos cualitativamente distintos —al menos, superficialmente—: la de juegos de azar donde existen fenómenos —tiradas de dados, juegos de naipes, extracción de bolas de colores de urnas, etc.— que se repiten.
El hecho de poder repetir un experimento aleatorio de esas características —y luego también de otros, como la medición de fenómenos en laboratorio, la toma de de datos astronómicos, etc.— dio lugar al concepto de muestra como colección de observaciones de una variable alteatoria.
Dos mismas muestras de una misma variable aleatoria pueden tener una apariencia externa distinta, como las dos siguientes:
s1 <- sample(1:6, 10000, replace = TRUE)
s2 <- sample(1:6, 10000, replace = TRUE)
head(s1, 100)## [1] 2 2 3 1 2 4 3 3 5 1 2 6 2 5 6 5 2 4 5 1 3 6 6 4 1 2 3 4 5 3 3 4 6 5 4 4 5
## [38] 4 2 3 2 3 4 2 4 2 2 1 4 6 2 3 5 6 1 5 3 6 3 3 2 2 5 1 6 5 4 6 3 3 4 1 1 2
## [75] 5 4 4 6 3 6 1 2 3 6 2 1 6 6 6 6 5 5 4 3 5 6 5 3 5 6head(s2, 100)## [1] 5 2 3 1 3 2 4 5 6 2 5 5 6 2 2 1 3 6 5 6 1 3 1 6 2 5 3 2 3 4 3 5 3 4 6 6 5
## [38] 2 3 4 2 5 5 3 3 4 4 4 5 3 1 4 4 1 2 5 2 1 5 6 6 4 4 5 4 4 4 1 5 2 5 4 4 6
## [75] 1 3 5 6 5 4 6 6 2 1 2 3 1 3 3 3 1 4 6 5 6 2 2 6 4 2Sin embargo, se encontró que la aparente disimilitud de muestras distintas de un mismo fenómeno aleatorio era posible encontrar sorprendentes regularidades. Por ejemplo,
mean(s1)## [1] 3.4959mean(s2)## [1] 3.5208son dos números parecidos. También, por ejemplo, la proporción (o frecuencia relativa) de unos en ambas muestras es similar
mean(s1 == 1)## [1] 0.1638mean(s2 == 1)## [1] 0.1646y, de hecho, muy similar a la probabilidad que le asocia el fenómeno aleatorio.
Esta vez, por construcción. Pero podríamos desconocer las probabilidades que asigna el fenómeno aleatorio a cada uno de los eventos y aun así obtener frecuencias relativas similares en distintas muestras.
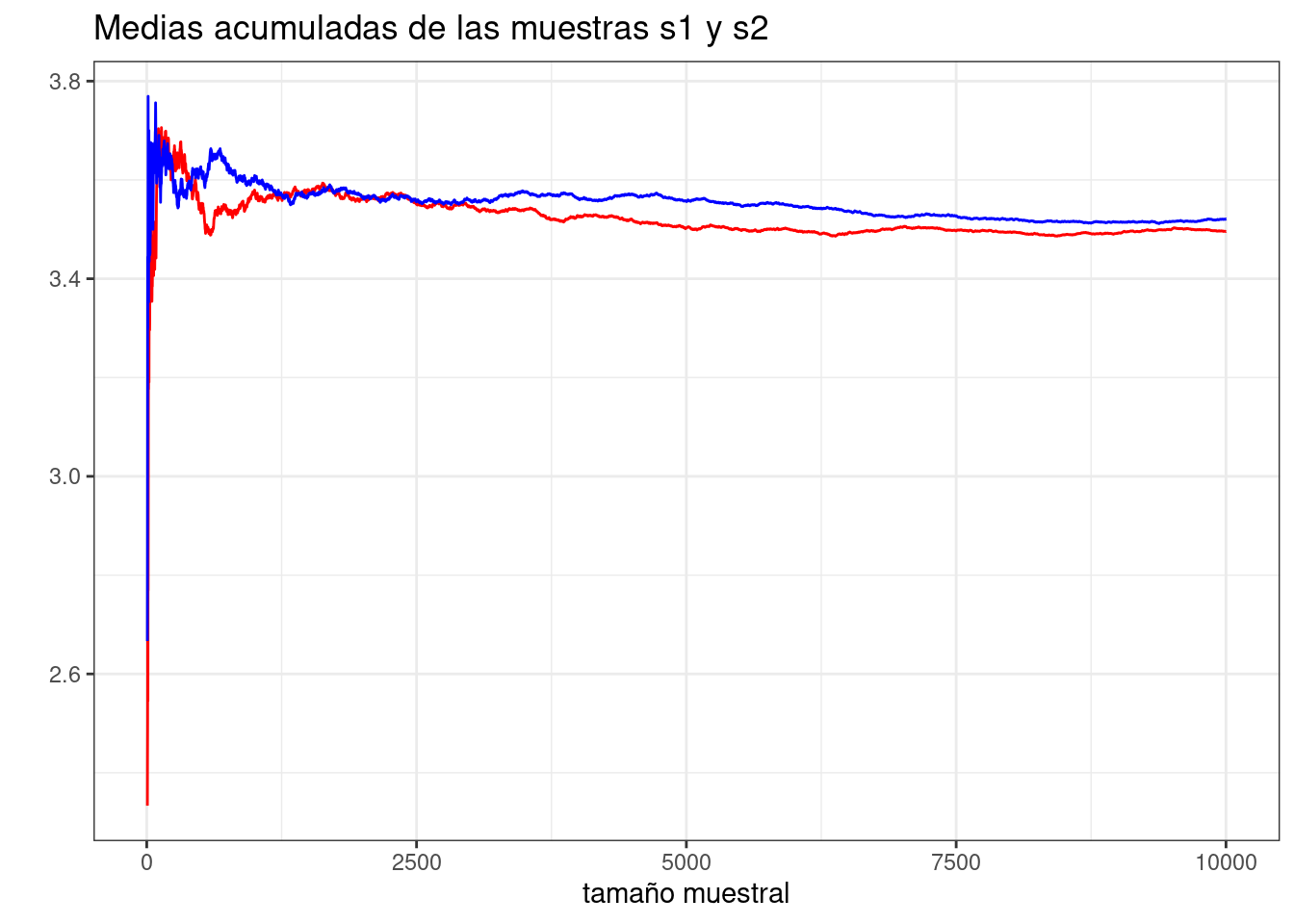
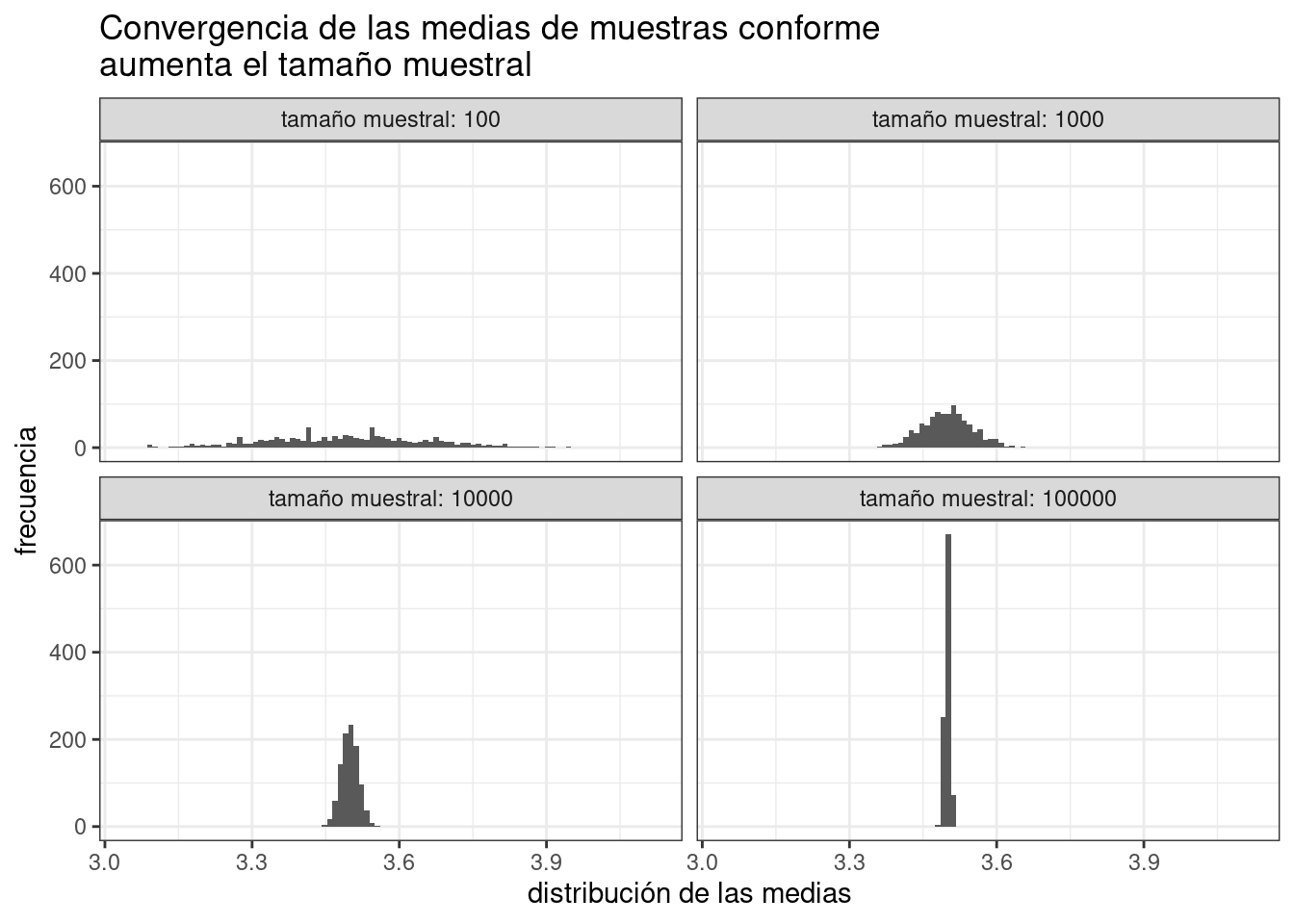
Estos resultados más o menos empíricos vinieron a recogerse históricamente bajo la —en algún momento de la historia— misteriosa y algo paradójica ley de los grandes números. La intuición imperante siglos atrás es que al analizar, tabular y promediar muestras procedentes de fenómenos aleatorios, se iban a encontrar igualmente agregados aleatorios. Así, en (Desrosières 2004), se lee:
La aplicación de la ley de los grandes números a la estabilidad de las medias calculadas (por ejemplo, la de las tasas de natalidad, matrimonio, crímenes o suicidios) impresiona a los contemporáneos de Quetelet y constituye el ensamblado de una macrosociología para la cual lo “social” tiene una realidad exterior y superior a los individuos: es la idea central de El suicidio de Durnkheim […].
Muy elocuentemente, un libro con un contenido e intención similar al de Desrosières es La domesticación del azar, de Ian Hawking, (Hacking 1990), cuyo título describe muy bien la intención de este capítulo.
Pero antes de explorar… una digresión necesaria.
4.2 La media y la varianza
Importantes, pero son como los andamios de una casa: aprenderemos a retirarlos.
4.2.1 La media
Supóngase que \(X\) es una variable aleatoria discreta que toma los valores \(x_1, \dots, x_n\) con probabilidades \(P(X = x_i) = p_i\). Entonces, la expresión
\[E[X] = \sum_i x_i p_i,\]
es lo que hoy llamamos la media o la esperanza de \(X\) pero que históricamente ha sido conocida con multitud de otros nombres pintorescos y descriptivos, como el centro de gravedad, el valor más probable, etc.
Ejercicio 4.1 Justificar que el nombre valor más probable es, en general, impropio. ¿Existe, no obstante, algún tipo de distribución para el que resulte adecuado?
Si \(X\) es una variable aleatoria y \(f\) es una función e \(Y\) es la variable aleatoria \(Y = f(X)\), entonces
\[E[Y] = \sum_i y_i P(Y = y_i) = \sum_i y_i P(\{x_j | f(x_j) = y_i \}) = \sum_j f(x_j) P(X = x_j),\]
resultado que en algunos lugares se conoce con el pintoresco nombre de la ley del estadítico inconsciente (Law of the unconscious statistician 2022). En concreto, de ella se deduce que \(E[\lambda X] = \lambda E[X]\) para cualquier número \(\lambda\).
La media es un operador lineal porque, además, \(E[X + Y] = E[X] + E[Y]\). Intuitivamente, si la fábrica \(A\) fabrica, en promedio, 100 unidades y la \(B\) 120, en promedio, conjuntamente, deberían fabricar 220. No obstante, es ilustrativo proporcionar una demostración matemática:
\[E[X+Y] = \sum_{ij} (x_i + y_j) P(X=x_i, Y = y_j) = \\ \sum_{ij} x_i P(X=x_i, Y = y_j) + \sum_{ij} y_j P(X=x_i, Y = y_j) = \\ \sum_i x_i P(X=x_i) + \sum_j y_j P(Y = y_j) = E(X) + E(Y)\]
En la expresión anterior se ha usado la marginalización de la distribución conjunta \(P(X=x_i, Y = y_j)\). En efecto,
\[\sum_{ij} x_i P(X=x_i, Y = y_j) = \sum_i x_i \sum_j P(X=x_i, Y = y_j) = \sum_i x_i P(X=x_i).\]
En resumen, la media es una característica de una variable alteatoria que da cierta idea de su valor central y que tiene propiedades matemáticas muy prácticas. Lo segundo, como se verá, ha hecho que se abuse de su utilización para lo primero. Más adelante se explorarán otras alternativas.
4.2.2 La varianza
Una manera de resumir sucintamente una variable aleatoria consiste en proporcionar un valor central —por ejemplo, su valor medio— y una medida de la dispersión de sus valores alrededor de dicho valor: ¿están todos próximos a él? ¿o existe una gran dispersión?
La varianza es una medida de dicha dispersión. La varianza de una variable aleatoria \(X\) con media \(\mu\) es, de hecho,
\[\text{Var}(X) = E[(X - \mu)^2] = \sum_i (x_i - \mu)^2 p_i,\]
es decir, el valor promedio de las distancias entre cada valor posible y la media. Con una elección muy particular, además, de la distancia, el cuadrado de la diferencia \(x_i - \mu\). Más adelante se estudiará la conveniencia de reemplazar esta distancia por otras medidas —¿por qué no \(|x_i - \mu|\) o, más en general, \(|x_i - \mu|^p\) para algún \(p > 0\)?— y sus consecuencias.
La varianza restringe de alguna manera la distancia a la que los valores de la variable aleatoria se pueden alejar de la media: una varianza pequeña obliga a que estén concentrados cerca de ella, etc. La desigualdad de Chebichev,
\[P(|X - \mu| > a) \le \frac{\text{Var}(X)}{a^2}\]
hace explícita esa relación: la probabilidad de los puntos alejados de la media no puede ser muy grande y está acotada por la varianza.
Chebichev demostró su desigualdad en 1867 (???) y la demostración es simple e instructiva: si \(X\) asume los valores \(x_1, \dots, x_n\) y \(x_1, \dots, x_m\) son los \(m\) valores de \(X\) tales que \(|x_i - \mu| \gt a\), entonces
\[P(|x_i - \mu| \gt a) = \sum_1^m p_i \le \sum_1^m \frac{(x_i - \mu)^2}{a^2}p_i \le \frac{1}{a^2} \sum_i^n (x_i - \mu)^2 p_i = \frac{\text{Var}(X)}{a^2}\]
Ejercicio 4.2 En realidad, no hay nada específico de la distancia cuadrática en la demostración anterior. Modifícala para alternativas de la varianza basadas en, por ejemplo, una distancia genérica \(|x_i - \mu|^p\) para algún \(p > 0\).
Ejercicio 4.3 Si \(X\) es una variable aleatoria con varianza \(\sigma^2\), ¿cuál es la varianza de \(\lambda X\)?¿Y la de \(X - \lambda\)?
La elección de la distancia cuadrática en la definición de la varianza, sin embargo, dota a la varianza de una serie de propiedades matemáticas muy deseables. La más importante de ellas es la siguiente: la varianza de la suma de dos variables alteatorias independientes es la suma de sus varianzas. En efecto, —y suponiendo, gracias al ejercicio anterior y por simplificar, que las variales aleatorias \(X\) e \(Y\) tienen media cero—
\[\text{Var}(X + Y) = E[(X + Y)^2] = E[X^2] + E[Y^2] + 2 E[XY] = \\ = \text{Var}(X) + \text{Var}(Y) + 2 E[XY],\]
y basta con demostrar que \(E[XY] = 0\) si \(X\) e \(Y\) son independientes.
Ejercicio 4.4 Demuestra el resultado anterior.
La expresión \(E[XY]\) (y en general, sin suponer que las medias son nulas, \(E[(X - E[X]) (Y - E[Y])]\)) es la llamada covarianza entre \(X\) e \(Y\). Dependiendo de si su covarianza es positiva o negativa, la varianza de la suma de variables aleatorias estará por encima o por debajo de la suma de sus varianzas.
Ejercicio 4.5 Una inversión de 100 euros en el activo financiero \(X\) tiene una varianza (p.e., mensual) de 10; y una inversión de 100 euros en \(Y\) tiene una varianza de 20. ¿Cuál es la varianza de una una inversión de 50 euros en \(X\) y 50 euros en \(Y\) si \(X\) e \(Y\) son independientes?
Uno de los objetivos de las finanzas es construir carteras de bajo riesgo. Una cartera, abstractamente, es una suma ponderada de variables aleatorias: las variables aleatorias son los activos que la componen, las ponderaciones, las inversiones realizadas en cada uno de los activos. Para reducir en la medida de lo posible la varianza de esta suma, es conveniente que la cartera esté integrada por activos con covarianzas bajas, idealmente cero o negativas.
4.3 La ley de los grandes números
Formalmente, una muestra \(x_1, \dots, x_n\) de una variable aleatoria \(X\) es un valor posible de una colección \((X_1, \dots, X_n)\) de variables aleatorias \(X_i\) independientes con la misma distribución que \(X\) y la ley de los grandes números concierne a la distribución de la variable aleatoria
\[Y = \frac{\sum_i X_i}{n}.\]
Si se supone que la media y la varianza de \(X\) existen y que son \(\mu\) y \(\sigma^2\), entonces, es inmediato constatar, primero, que \(E[Y] = E[X] = \mu\); y por otra parte, que
\[\text{Var}(Y) = \frac{1}{n^2} \sum_i \text{Var}(X_i) = \frac{\sigma^2}{n}.\]
Por lo tanto, aplicando la desigualdad de Chebichev,
\[P\left(\left|\frac{\sum_i X_i}{n} - \mu \right| > a \right) \le \frac{\sigma^2}{na^2},\]
es decir, que si \(n\) es lo suficientemente grande, cabe esperar (o es muy probable) que
\[\frac{\sum_i X_i}{n} \sim \mu.\]
Esta es la versión de la ley de los grandes números probada por Chebichev en 1867. Existen otras en que se relaja la condición de la existencia de la varianza de \(X\), se garantiza la llamada convergencia en casi todo punto, o se permite cierto grado de dependencia entre las variables aleatorias \(X_i\). Pero esta será suficiente en todo lo que sigue.
Así que cabe esperar que las medias de los valores muestrales
\[\frac{\sum_i x_i}{n}\]
converjan al valor medio \(\mu\). Pero la ley de los grandes números también garantiza por ejemplo, que si \(Y\) es la variable aleatoria que toma el valor \(1\) si \(X = a\) y \(0\) en otro caso, la media de muestras de \(Y\) converjan a \(P(X = a)\). Por eso, por ejemplo, si se hace
s0 <- sample(1:6, 10000, replace = TRUE)(para simular lanzamientos de dados), la media de
s1 <- s1 == 5(una muestra de la variable aleatoria indicadora del evento \(X=5\)), tendrá que ser próxima a \(1/6\). Y, en efecto,
mean(s1)## [1] 0.1678Por el mismo motivo convergen los histogramas (si se permite la expresión tal vez no lo suficientemente formal). Dada una muestra de una variable aleatoria \(X\) (esta vez no necesariamente discreta), su histograma es una representación parecida a
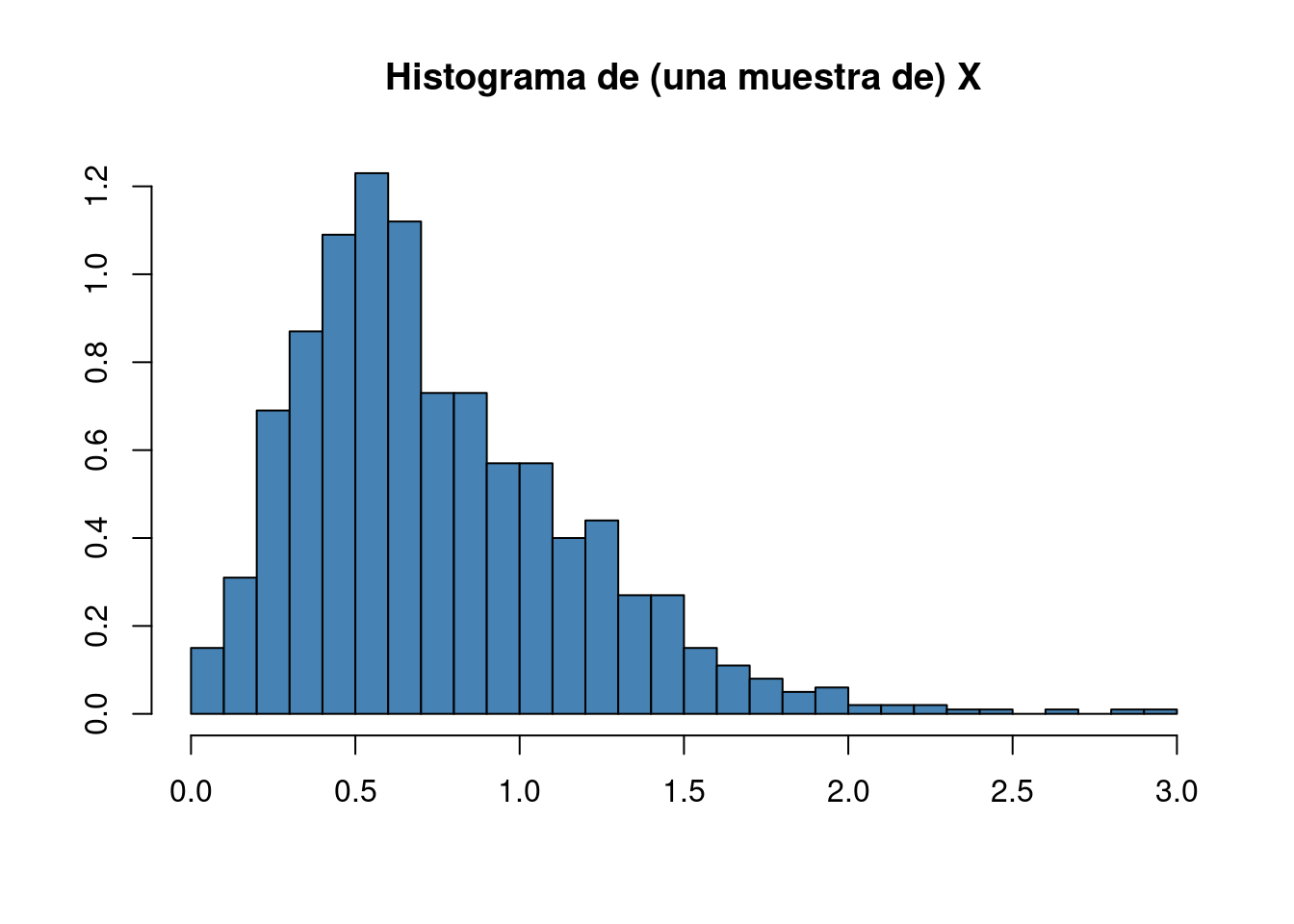
donde el área de cada rectángulo es proporcional a la proporción de valores de la muestra que toman valores en su base. Por la discusión anterior, esa proporción tenderá al valor real de la probabilidad de que \(X\) tome valores en dicho segmento. Es la ley de los grandes números la que garantiza, por un lado, que los histogramas de muestras distintas de una misma distribución tengan aspectos similares y, por el otro, que podamos hablar, como se hará en un capítulo posterior, del límite de los histogramas.
4.4 Simulaciones
Las implicaciones prácticas de estos resultados son enormes. La más importate de ella es que —en casi cualquier circunstancia real—, para resolver problemas prácticos, no será necesario desarrollar cálculos muchas veces complejos tediosos sino que será posible simular.
Por ejemplo, ¿cuál es la probabilidad de que al tirar tres dados se obtenga un resultado de 10? Contando cuidadosamente se llega a la conclusión de que existen 27 casos favorables en un total de \(6^3 = 216\) posibles resultados, es decir, que la probabilidad es como del 12.5%. Pero esa es la misma respuesa que da, casi inmediatamente,
tmp <- matrix(sample(1:6, 3 * 1e6, replace = TRUE), 3, 1e6)
mean(colSums(tmp) == 10)## [1] 0.124706Otro ejemplo un poco más sofisticado está motivado por un episodio de la serie de televisión coreana El juego del calamar. Los participantes del juego tienen que atravesar un precipicio a través de un puente. Este puente está formado por 20 parejas de losas de cristal. En cada pareja de losas, una de ella es sólida y aguanta el peso del jugador; la otra es frágil, cede y el jugador que salta en ella se precipita al abismo.
El primer jugador puede elegir saltar a una de las dos parejas de losas. Si acierta con la sólida, puede seguir intentándolo con la siguiente. Los demás jugadores lo siguien por el puente. En el momento en el que el primer jugador se precipita, el segundo de la fila pasa a relevarlo.
Obviamente, el primer jugador tiene una probabiliad de 1 / 2^20 (1 entre un millón, aproximadamente) de superar con éxito (o vida) la prueba. El jugador 21, por su parte, sabe que va a superarla necesariamente. ¿Cuál es la probabilidad de que la fallezcan, por ejemplo, 10 jugadores?
El valor simulado
sample(0:1, 20, replace = T)## [1] 1 1 1 1 0 1 1 1 0 0 1 0 0 0 0 1 0 1 0 0puede representar una realizazión el juego en el que los unos significan que alguien saltó a la losa equivocada. La suma de esos valores representa, por tanto, el número de jugadores fallecidos en una realización. Por lo tanto,
n <- 1e5
res <- replicate(n, sum(sample(0:1, 20, replace = T)))
table(res) / n## res
## 1 2 3 4 5 6 7 8 9 10
## 0.00002 0.00015 0.00119 0.00500 0.01457 0.03790 0.07387 0.11964 0.15987 0.17618
## 11 12 13 14 15 16 17 18 19
## 0.16188 0.11839 0.07322 0.03739 0.01443 0.00495 0.00111 0.00020 0.00004proporciona la probabilidad aproximada de cada número de fallecidos.
Más adeante se verá que esta simulación es muy ineficiene y que, de hecho, puede obtenerse una probabilidad exacta recurriendo a la distribución binomial. Las probabilidades exactas son
x <- 0:20
p <- dbinom(x, 20, .5)TODO: simulación de la fase de grupos del mundial.
4.5 Bondad de las aproximaciones y teorema central del límite
Queda un pequeño problema por resolver antes de abrazar metodológicamente los métodos basados en muestreos: la estimación del error cometido o, lo que viene a ser lo mismo, la determinación del número necesario de simulaciones para obtener una aproximación razonable.
La acotación del error nos la da, parcialmente, el llamado teorema central del límite. Este teorema estudia, de hecho, la bondad de la aproximación de las medias a su límite. Por la ley de los grandes números,
\[Y_n = \frac{\sum_i X_i}{n}\]
tiene media \(\mu\) y varianza
\[\text{Var}(Y_n) = \frac{\sigma^2}{n}.\]
Entones, la variable aleatoria
\[\sqrt{n}\;(Y_n - \mu)\]
tiene media cero y varianza constante. Eso quiere decir que la distancia cuadrática promedio —recuérdese la discusión acerca de la función de distancia usada en la definición de la varianza— entre \(\sqrt{n}(Y_n - \mu)\) y 0 es constante o bien que la distancia promedio entre \(Y\) y \(\mu\) decrece como \(1/\sqrt{n}\).
De hecho, el teorema central del límite garantiza más: de cumplirse una serie de condiciones habituales en la práctica, \(Y - \mu\) tiene una distribución aproximadamente normal de media \(0\) y varianza \(\sigma^2 / n\) (o bien, que \(Y\) tiene, aproximadamente, una distribución normal de media \(\mu\) y y varianza \(\sigma^2 / n\)).
Lo más importante que tener en cuenta, en todo caso, es que el error producto de las simulaciones decrece con \(1/\sqrt{n}\).
4.6 Bibliografía razonada
Referencias para la ley de los grandes números, teorema central del límite, etc. Decir que aquí se ha probado la versión más débil, aunque suficiente para casi todos los fines.
Hablar algo de la historia de estos teoremas. ¿De quién son?
Hablar del rol “atractor” de la distribución normal.
4.7 Ejercicios
Ejercicio 4.6 Supóngase una inversión de 100 euros los activos financieros \(X\) e \(Y\) tiene varianzas (p.e., mensuales) \(\sigma_X^2\) y \(\sigma_Y^2\). Si \(X\) e \(Y\) son independientes, ¿cuál es la proporción de 100 euros que hay que invertir en \(X\) para miniminzar la varianza de la cartera conjunta?
Ejercicio 4.7 Uno con la convergencia (o no) con la distribución de Cauchy. TODO: ¿moverlo más arriba para que se vea el contraejemplo pronto?
Referencias
Desrosières, A. 2004. La Política de Los Grandes Números. Editorial Melusina.
Hacking, I. 1990. The Taming of Chance. Ideas in Context. Cambridge University Press.
Law of the unconscious statistician. 2022. “Law of the Unconscious Statistician — Wikipedia, the Free Encyclopedia.” https://en.wikipedia.org/w/index.php?title=Law_of_the_unconscious_statistician&oldid=1112046836.