Una paradoja que no me parece paradójica, la de Bertrand, y una pregunta
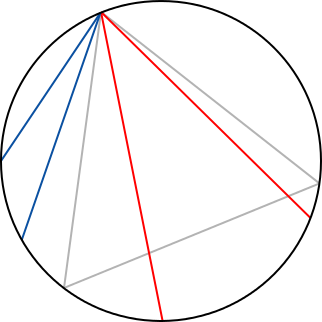
La paradoja de Bertrand se formula así: tómense una cuerda al azar en una circunferencia; ¿cuál es la probabilidad de que sea más larga que el lado del triángulo equilátero inscrito?
Bertrand resolvió el problema de tres maneras distintas obteniendo tres resultados distintos: 1/2, 1/3 y 1/4. ¿Es eso una paradoja?
La paradoja es consecuencia de que no existe una definición única de cuerda al azar, algunas de las cuales acaban dando más peso a cuerdas más largas y otras menos. En resumen, hay varias maneras razonables de muestrear cuerdas de circunferencias y los resultados pueden ser distintos.
Y si en lugar de cuerdas muestreamos españoles (por ejemplo, para encuestarlos sobre su opinión sobre los toros), ¿habrá también mecanismos de muestreo distintos que den lugar a resultados igualmente distintos?