De ratios, apuestas y riesgos

Nunca he entendido eso de los odds. Me refiero a eso que mencionan las películas: ocho contra uno a favor de tal, cinco contra tres a favor de cual. Y no creo que sea el único al que le son ajenos. De hecho, la página de la Wikipedia en español correspondiente a la inglesa para odds se refiere a ellas como cuotas, término que jamás hasta hoy había visto así usado. Tampoco lo han visto, se concoce, los lexicógrafos de la RAE.

Entender lo de los odds —dejadme que los llame así— me ha llevado un ratillo. En la Wikipedia se menciona un ejemplo: en una competición hay tres participantes que tienen probabilidades de ganar iguales a 0.5, 0.4 y 0.1. Sus correspondientes odds son 1:1, 3:2 y 9:1. Esto es así porque, por ejemplo, para el tercer participante, 1 / (1+9) = 0.1. En general, para odds a:b, la probabilidad del evento es b/(a+b).

Dicho lo cual, ¿soy el único que prefiere las probabilidades a los odds y las ve más naturales?

Peor aún, existe eso que llaman el odds ratio (OR, por abreviar). El OR entre los dos últimos participantes del ejemplo anterior sería (2/3)/(1/9) = 6. ¿Nadie ve más natural decir que el primero tiene 4 veces más probabilidades de ganar que el segundo? No sé.

Lo que nos conduce a la siguiente cuestión: ¿por qué hablamos tanto del OR en estadística (y sus aplicaciones)? Pues es por culpa del instrumento (o uno de los instrumentos) que usamos para calcular probabilidades, la regresión logística. Es como si los coches midiesen la distancia en términos del número de vueltas que dan las ruedas y no de kilómetros.

En el modelo logístico el coeficiente de una variable binaria (p.e., “tabaco”) es el logaritmo del OR. En este caso, el ratio lo es entre los casos en los que dicha variable es 1 y el caso base (donde es 0). En efecto

$$ p_1=\exp(\dots+1\beta+\dots)/(1+\exp(\dots+1\beta+\dots))$$

y

$$ p_0=\exp(\dots+0\beta+\dots)/(1+\exp(\dots+0\beta+\dots)=\exp(\dots)/(1+\exp(\dots))$$

Despejando,

$$ \exp(\dots+\beta+\dots)=p_1/(1-p_1)$$

y

$$ \exp(\dots)=p_0/(1-p_0)$$

por lo que

$$ exp(\beta)=\frac{p_1/(1-p_1)}{p_0/(1-p_0)}$$,

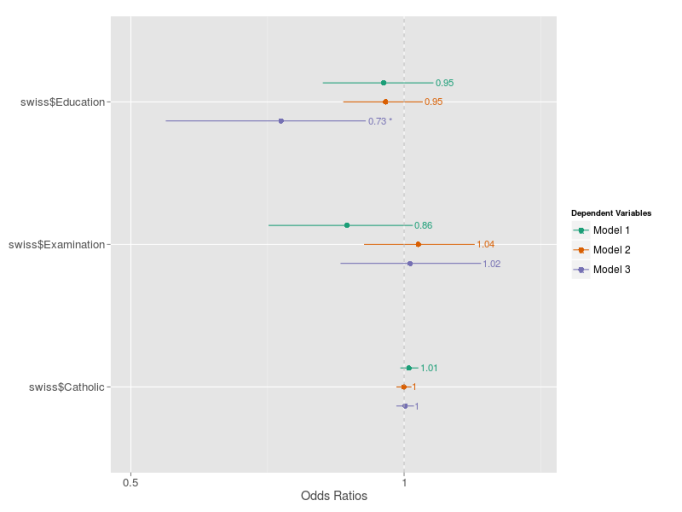
nuestro OR. Y claro, como $latex \beta$ tiene asociados intervalos de confianza, etc. uno puede hacer estadística y, por ejemplo, construir gráficos tales como

(Nota: el gráfico anterior está extraído de aquí, la bitácora del autor del paquete sjPlot, con el que se ha generado el gráfico anterior).

Pero, como he discutido más arriba, el OR es difícilmente interpretable (salvo que seas un inglés aficionado a las carreras de galgos).

¿Qué alternativas existen?

Las que más me gustan requieren dos números: la probabilidad del caso base y la probabilidad del caso de interés. Pero tanta cifra atraganta a la gente: los más quieren solo un número. Aunque sea la media. Satisfagámoslos entonces.

Habiendo dos números de interés (las dos probabilidades) una cosa que puede hacerse para dejarlos en uno es dividirlos. A ese cociente se lo llama riesgo relativo. Puede calcularse a partir del or (y de la probabilidad del caso base) como se indica aquí. Quienes dispongan de un boli, una servilleta y un bachillerato cursado con aprovechamiento no necesitarán siquiera seguir el enlace.

Finalmente, que algo sea x veces más probable que otra cosa tampoco es tremendamente relevante si las probabilidades son ínfimas. Por ejemplo, pueden decir que quienes toman el medicamento A tienen 7 veces más probabilidad de sufrir X que los que no. ¿Pero qué si X solo ocurre a una persona de cada millón?

Por concluir, dejo como ejercicio la lectura de este artículo de Spiegelhalter sobre mecanismos human friendly de expresar riesgos relativos (y, por extensión, comparar probabilidades).