Modelización de retrasos: una aplicación del análisis de supervivencia

En vigilancia epidemiológica contamos eventos (p.e., muertes o casos de determinadas enfermedades). Lo que pasa es que el caso ocurrido en el día 0 puede notificarse con un retraso de 1, 2, 3… o incluso más días. En algunas aplicaciones, incluso semanas.

¿Cómo estimar el número de casos ocurridos el día 0 el día, p.e., 5?

Se puede aplicar el análisis de la supervivencia donde el evento muerte se reinterpreta como notificación. El el día 0 todos los sujetos están vivos y, poco a poco, van cayendo. Como en los consabidos modelos/gráficos de Kaplan-Meier,

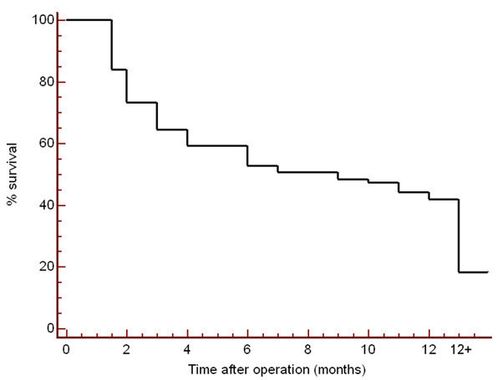
Incluso, si el retraso puede atribuirse a distintos factores (por ejemplo, el día de la semana en que se produce el evento porque la gente que los comunica deja caer el boli el viernes a las tres), pueden construirse distintas curvas, como en

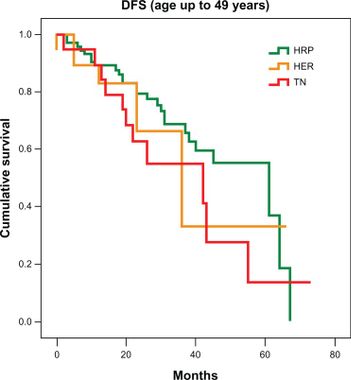
Hecho lo cual, ¿cómo estimar el número de casos del día 0 el día, p.e, 5? El modelo proporciona la proporción de notificados, $latex x$. Así que se hace una regla de tres y si a $latex x$ le corresponden $latex n$ notificados, a 1 le corresponderán… $latex n/x$.

Pues no, no, no, no… ¡no!

Ese modelo trivial es más inestable que el carajo. ¡Imaginad como puede bailar ese estimador cuando $latex x$ es del orden del 1%!

Es mucho mejor utilizar un suavizado (de inspiración bayesiana). Si $latex m$ es el número medio de notificaciones diarias, es mucho mejor utilizar

$$ n + (1 - x) m$$

que vendría a ser un promedio de nuestro modelo anterior con peso $latex x$ y otro modelo más simple (con peso $latex 1 -x$) que asigna a cada día un número de notificados igual a la media histórica.

Así funciona (y no siempre tan bien como sería deseable) esto, de donde extraigo

Nota: En el gráfico hay algo más, un poco más, que es lo que permite construir intervalos no muy confiables de confianza alrededor del estimador construido más o menos como se indica arriba.

Otra nota: Este es el tipo de cosas que hacemos en Circiter y gracias a las cuales nos distinguimos (muy favorablemente) de otras empresas donde, bueno,… la estadística… Callaré, mejor.