Una pregunta sobre pruebas de hipótesis

Más que pregunta, debería haberlo planteado como encuesta: no estoy preguntando sino preguntándote qué es lo que haces tú (habitualmente).

Va de pruebas de hipótesis (a la Fisher). La teoría dice que hay que plantear una hipótesis nula y para poder estudiar lo anómalos que son los datos obtenidos experimentalmente bajo dicha hipótesis. Es decir, calculas $latex P(X | H_0)$.

Alternativamente (en muchos contextos, no en todos: no sabría cómo hacerlo, p.e., con el ks.test) uno puede echarle un vistazo a los intervalos de confianza del parámetro de interés y ver si incluye o no el valor de referencia.

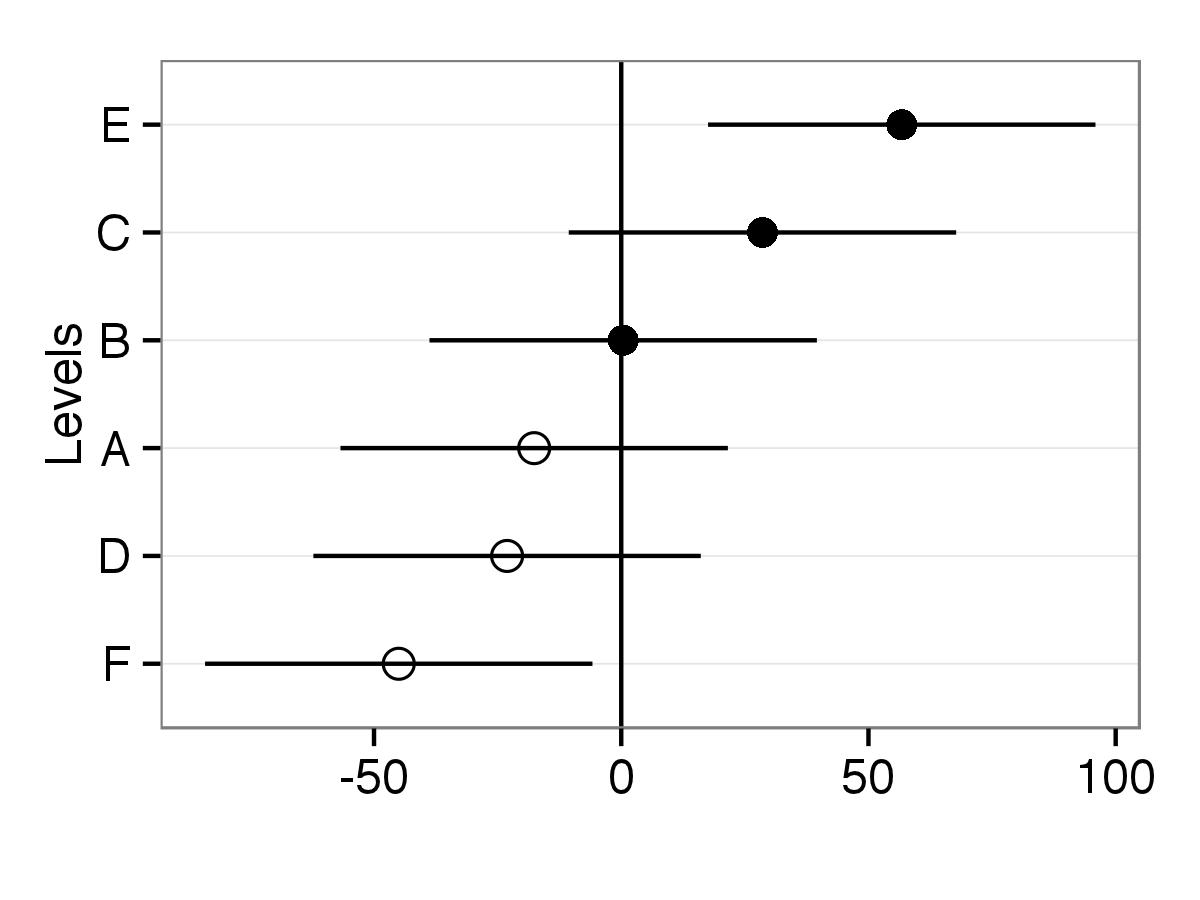
La pregunta, es: ¿qué sueles hacer tú? ¿Dónde aplicas un tipo de pruebas y dónde el otro?

Si te gustan más los intervalos de confianza, ¿por qué? ¿Cómo lo justificas? Porque Fisher nunca habló de intervalos de confianza, ¿o sí?