El extraño caso de la media empírica menguante

La distribución lognormal es la exponencial de una distribución normal. Su media, Wikipedia dixit, es $latex \exp(\mu + \sigma^2 /2)$.

Dada una muestra de la distribución lognormal (y supuesto, por simplificar, $latex \mu=0$), podemos calcular

• su media y
• una estimación de su $latex \sigma$ y calcular $latex \exp(\sigma^2 /2)$

y uno pensaría que los valores deberían ser similares. Mas pero sin embargo,

library(ggplot2)

set.seed(123)

sigmas <- seq(1, 10, by = 0.1)

res <- sapply(sigmas, function(sigma){
  a <- exp(rnorm(1e6, 0, sigma))
  mean(a) / exp(var(log(a))/2)
})

tmp <- data.frame(sigmas = sigmas, medias = res)

ggplot(tmp, aes(x = sigmas, y = medias)) +
  geom_point() + geom_smooth()

produce

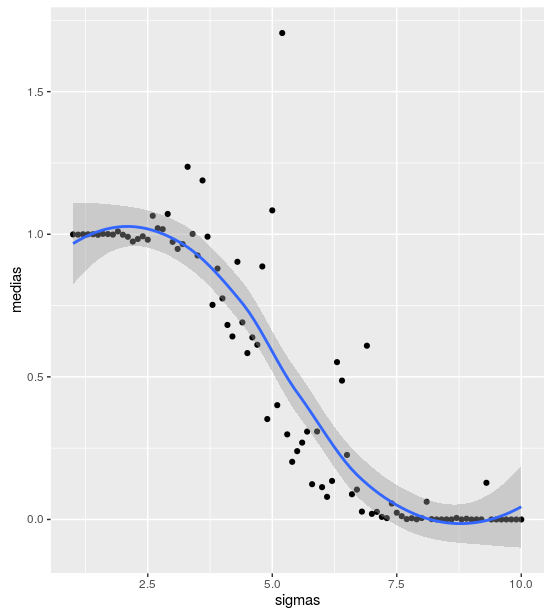
El gráfico anterior, para quien tenga pereza de desentrañar el código, muestra la razón entre la media empírica y la teórica para una serie de extracciones de un millón de muestras de una distribución lognormal con parámetro $latex \mu = 0$ y con $latex \sigma$ variando entre 0 y 10. Dicha razón, como cabría esperar, se mantiene cerca de uno para valores bajos de $latex \sigma$, pero se derrumba para valores más altos.

El asunto es relevante porque el comportamiento proyectado a futuro de muchas series de importancia económica (p.e., cotizaciones bursátiles, aunque sospecho que también otras como el PIB y similares) encuentran en la distribución lognormal una aproximación. No son estrictamente lognormales, pero es frecuente encontrar quien da dicha aproximación, tal vez con algún caveat, por buena. Además, sospecho que aquellos aspectos cualitativos que uno podría esgrimir para descalificar el recurso a la lognormal tenderían a acentuar la desviación que motiva esta entrada. Lo cual significaría que en situaciones de alta volatilidad, la rentabilidad del común de los mortales quedaría muy por debajo de la media y algún afortunado se lo llevaría crudo.

Y como este último párrafo, el de la conclusión, debería tener contenido político, lo omito.