Análisis estadístico de respuestas ocultas en encuestas

A veces se hacen encuestas sobre temas sobre los que los encuestados son reticentes a revelar la verdad (p.e., ¿es Vd. un zombi?). Un procedimiento conocido para recabar tal tipo de información es el siguiente:

• Se le invita al encuestado a tirar al aire una moneda con las caras etiquetadas con sí y no; la moneda no es una moneda porque tiene una probabidad conocida (y distinta del 50%) de caer en sí.
• El encuestado responde sí si la respuesta a la pregunta y el resultado de la tirada de la moneda coinciden y no en caso contrario.

A partir de la proporción de respuestas positivas y conocida la probabilidad del sí de la moneda, $latex q$, es posible estimar la proporción $latex \theta$ de respuestas positivas a la pregunta de subyacente de interés en la muestra. Efectivamente, los síes tienen una distribución binomial $latex B(p) = B(q\theta + (1-q)(1-\theta))$ y, una vez estimado (por máxima verosimilitud) $latex \hat{p}$, puede despejarse $latex \hat{p}$ de $latex \hat{p} = q\hat{\theta} + (1-q)(1-\hat{\theta})$ para obtener

$$ \hat{\theta} = \frac{1 - q - \hat{p}}{1 - 2q}.$$

Así,

set.seed(12)
n <- 10000
unknown.par <- 0.2
coin.par    <- 0.3
biased.coin <- rbinom(n, 1, coin.par)
hidden.res  <- rbinom(n, 1, unknown.par)
results <- as.numeric(hidden.res == biased.coin)
get.theta <- function(p, q) (1 - p - q) / (1 - 2*q)
get.theta(mean(results), coin.par)
# 0.19

Y todo es estupendo.

¿Y si queremos intervalos de confianza, etc., del parámetro estimado? Podemos muestrear una $latex B(\hat{p})$ y ver cuál sería la distribución resultante de $latex \theta$:

muestras <- replicate(1000,
  mean(rbinom(n, 1, unknown.par) == biased.coin))
muestras <- sapply(muestras, function(x)
  get.theta(x, coin.par))
hist(muestras)
# etc.

Pero el procedimiento anterior tiene algunos caveats:

• La función get.theta es algo inestable: nada garantiza siquiera que dé valores positivos; de hecho, en algunas pruebas, me ha dado valores negativos en algunas ocasiones.
• Ni siquiera yo entiendo demasiado bien por qué, a la hora de hacer simulaciones, muestreo $latex B(\hat{p})$: ¿por qué $latex \hat{p}$ y no otro valor? Porque sé que la estimación de $latex \hat{p}$ está sujeta a error, etc.
• Hay gente que no sabría despejar $latex \hat{\theta}$

Afortunadamente, existe un procedimiento alternativo:

library(rstan)
standat <- list(N = n, pcoin = coin.par, x = sum(results))

stanmodelcode <- '
data {
  int<lower=1> N;
  real pcoin;
  int x;
}
parameters {
  real<lower=0, upper = 1> theta;
}
model {
  // prior (no informativa)
  theta ~ beta(1,1);
  // verosimilitud
  x ~ binomial(N, theta*pcoin + (1-theta)*(1-pcoin));
}
'
fit <- stan(model_code = stanmodelcode,
            data = standat,
            iter=12000, warmup=2000,
            chains=4, thin=10)
tmp <- as.data.frame(fit)
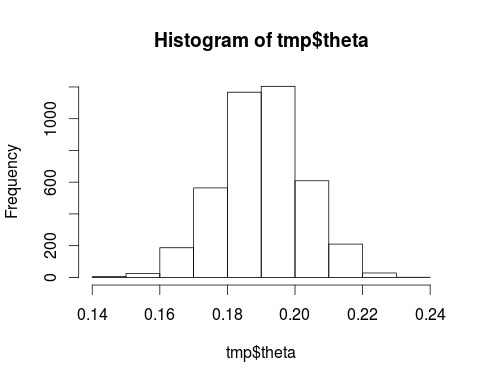
hist(tmp$theta)

Que genera

sin mayores complicaciones (ni teóricas ni prácticas). Además, como ventaja adicional, uno siempre puede incluir la información previamente conocida sobre la distribución de $latex \theta$ en el lugar correspondiente en el código anterior.