Un curioso corolario (políticoeconómico) del teorema de Rolle
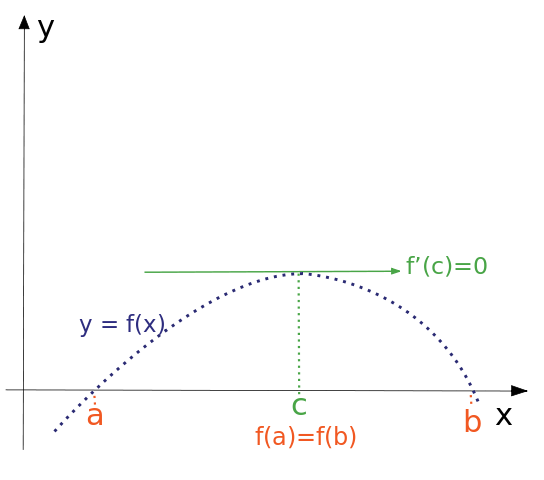
El teorema de Rolle, que está en el programa de cálculo o análisis matemático de primero de cualquier carrera, dice que una función real $latex f$, continua, derivable y tal que $latex f(a) = f(b)$ tiene o un máximo o un mínimo en el intervalo $latex [a,b]$. La Wikipedia lo ilustra con el siguiente gráfico:
Supongo que no será muy díficil de probar este corolario suyo (y creo recordar que fue un ejercicio o problema de examen de aquella época mía de estudiante): una función real $latex f$, continua, derivable y tal que $latex f(a) = f(b)$ y $latex f^\prime(x) < 0$ en la proximidad de $latex b$ tiene un máximo absoluto en el intervalo $latex (a,b)$.
¿Y el corolario políticoeconómico? Supongamos que $latex f$ es (¿es medible?) el bienestar social en España. Indiscutiblemente, $latex f(2015) > f(1750)$, por ejemplo. Según algunos, $latex f^\prime < 0$ en los últimos años. Y no solo los de la era de Rajoy, sino también la de Zapatero, Aznar, Felipe González… Pero el corolario indica entonces que hubo un máximo entre 1750 y 2015 del que los defensores del decrecimiento de $latex f$ estarán, supongo, nostálgicos. ¿En qué año —les pregunto, me pregunto— sitúan ese máximo?