Como no tengo tiempo, voy a publicar una chorrada (y una coda)

Como no tengo tiempo, voy a publicar una chorrada. Voy a coger unos datos que encuentre por ahí, voy a tomar alguna variable, voy a pintarla (en un mapa, si puede ser) y luego voy a construir una narrativa. Espero que no os deis cuenta y me lo creáis todo.

Comienzo.

Los datos del World Values Survey (aquí podéis obtenerlos) son mú importantes y mú guays. De todas las variables que contiene, voy a extraer una, la variable mú importante (VMI).

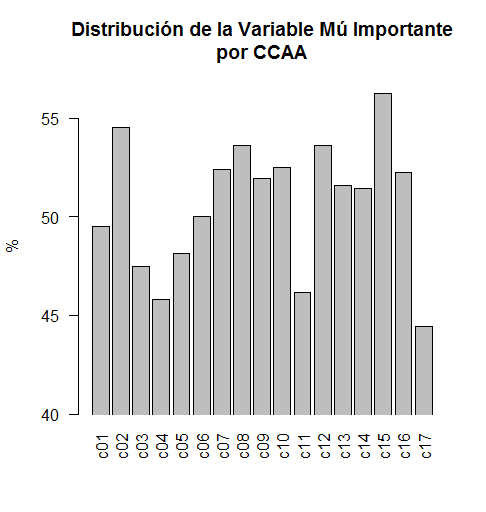
La VMI es muy importante, como su nombre bien indica. Se ha usado en la mar de estudios, publicados y no, en las más diversas disciplinas. Me interesa hoy conocer su distribución en función de, por ejemplo, la comunidad autónoma en España. Así es:

Verse puede cómo varía enormemente. En unas comunidades autónomas la barra es más alta, p.e., en la C15; en otras, más baja. Es muy baja en la C17, pero, ¿qué se puede esperar de la gente de la C17? ¡Si son todos de pueblo! Y no ni he ido ni quiero ir a la C17 jamás. ¿Para qué? Si despuntan en algo es en la variable mú importante… y para lo malo. Que yo sepa nunca salió de allá nada de provecho. Luego hay otras comunidades autónomas que están in medio, donde stat virtus. Ya lo decía Sancho Panza: tanto se pierde por carta de más como por carta de menos. Entre ellas se cuentan la próspera C06 y la C01. A pesar de que los de la C01 son un poco raritos, que conste.

Etc.

Y mañana más.

Coda

Obviamente, estoy de coña. Yo nunca escribiría algo así. Para eso, hago lo de ayer y me planto. Pero hay gente con menos vergüenza que la mía. Por ejemplo, la autora de esto.

Pinta ella cosas del tipo

que viene a ser una versión de mi gráfico de barras (¿os habéis fijado que, adrede, las barras no principian donde deben, en 0? ¡lo que me ha costado construirlo!) un poquito más elaborada —hay gente que tiene más tiempo que yo— y que tiene sobre el mío la ventaja de que nos recuerda la forma de Extremadura. Por lo demás, tanto el gráfico y las cifras que representa, como la inanidad de la narrativa que lo rodean en la publicación original son idénticos al mío.

¿Veis las diferencias tan notables que muestra el mapa anterior? ¿Serán significativas? Volveré a eso luego, pero quiero indicar primero que las variaciones en mi gráfico son espurias. La VMI que he representado es… la proporción de mujeres. Que varía mucho menos entre comunidades autónomas (INE dixit):

floor(fivenum(sexos$prop) * 10000) / 100
#[1] 49.65 50.24 50.49 51.07 52.10

Si con una variable conocida podemos detectar una varianza tan grande, ¿de verdad podemos fiarnos de los resultados que afectan a otras desconocidas? ¿No estaremos creando narrativas alrededor de ruido estadístico?

El problema es consencuencia, en parte, del minúsculo tamaño muestral. Véase el número de encuestas por comunidad autónoma:

sort(table(vmi$ccaa))
#c17 c06 c15 c04 c11 c02 c14 c03 c07 c05 c16 c08 c12 c10 c13 c09 c01
#  9  16  16  24  26  33  35  40  42  54  67  69  69 141 159 181 208

Después de lo cual, ahora más constructivamente, regreso al párrafo con el que la autora acompañaba el gráfico anterior,

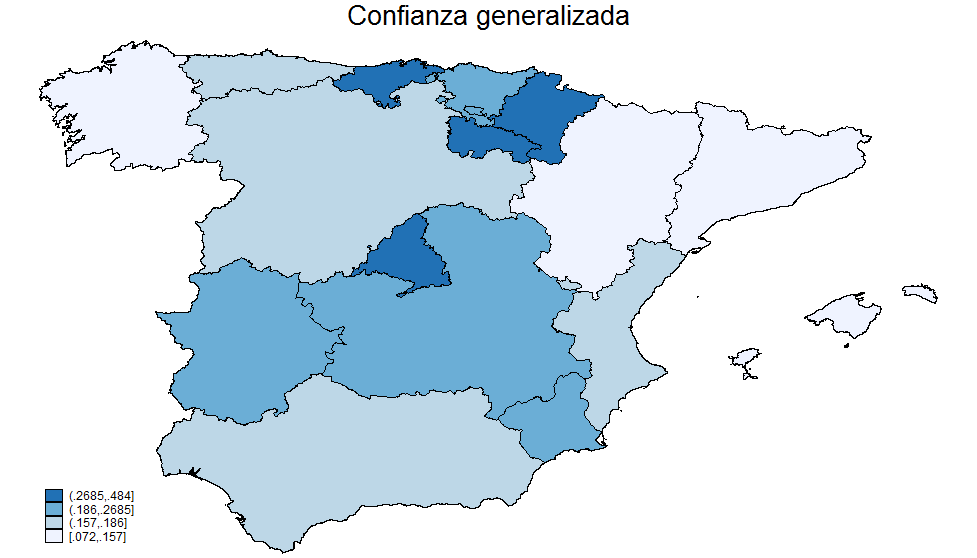
Confianza generalizada: Numerosos estudios han demostrado que el grado de “confianza generalizada” en una sociedad está fuertemente correlacionado con el desarrollo económico. Esta variable se mide con las respuestas a la pregunta: “En general, ¿diría usted que la mayoría de la gente es de fiar, o que hay que tener mucho cuidado en el trato con otra gente?”. De los encuestados en España, sólo el 19% afirmaba que la mayoría de la gente es de fiar. El mapa siguiente muestra considerable variación entre regiones (en todos los mapas, los cuatro colores dividen las regiones en cuartiles). El grado de confianza es relativamente bajo en Galicia, Cataluña, Aragón y Baleares, y alto en Madrid, Cantabria, La Rioja y Navarra.

y voy a ensayar un análisis utilizando técnicas de esas que, se conoce, no se enseñan en econometría nos enseñan quienes saben del asunto.

Inspirado por el artículo anterior, hago

library(lme4)
library(lattice)

# los datos están disponibles
# en http://www.worldvaluessurvey.org/
load("WorldValuesSurvey-Wave6-2010-2014_v2014-11-07.rdata")

wvs.all <- get("WorldValuesSurvey-Wave6-2010-2014_v2014-11-07")
spain <- wvs.all[wvs.all$V2 == 724,]

tmp <- spain[,c("V256", "V240", "V242", "V24")]
colnames(tmp) <- c("ccaa", "sex", "age", "trust")

tmp <- tmp[tmp$trust > 0,]
tmp$ccaa <- gsub("7240", "c", as.character(tmp$ccaa))

tmp$sex <- factor(tmp$sex)

mod3 <- lmer(<a href="http://inside-r.org/packages/cran/trust">trust ~ 1 + (1 | ccaa), data = tmp)
dotplot(ranef(mod3, condVar = TRUE))
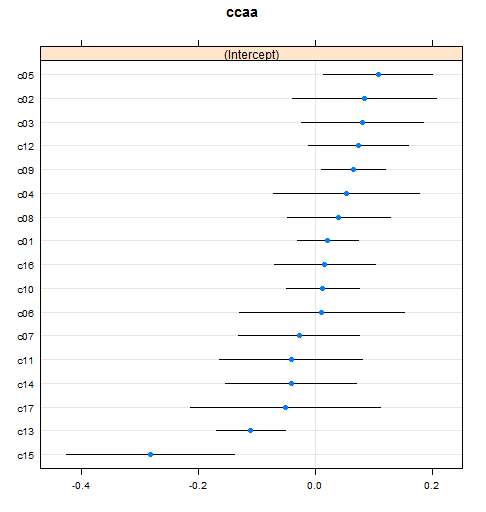
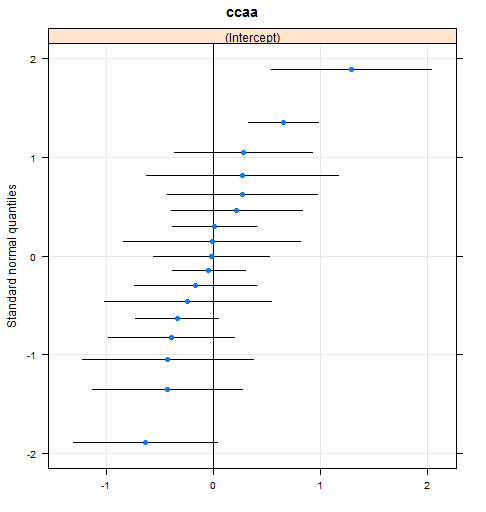
qqmath(ranef(mod3, condVar = TRUE))

para obtener

y

que nos indican que solo habría dos o tres comunidades en las que las diferencias en la variable confianza son realmente distintas de la media. Siendo la más extrema Navarra, en la que la diferencia (por eso el coeficiente tiene más variabilidad) está basada en apenas 15 encuestas.

Aunque bien podría argumentarse que lo que piden los datos es un modelo basado en glmer,

tmp$trust.bin <- tmp$trust == 1

mod.glmer <- glmer(trust.bin ~ 1 + (1 | ccaa),
                    family = binomial, data = tmp)
dotplot(ranef(mod.glmer, condVar = TRUE))
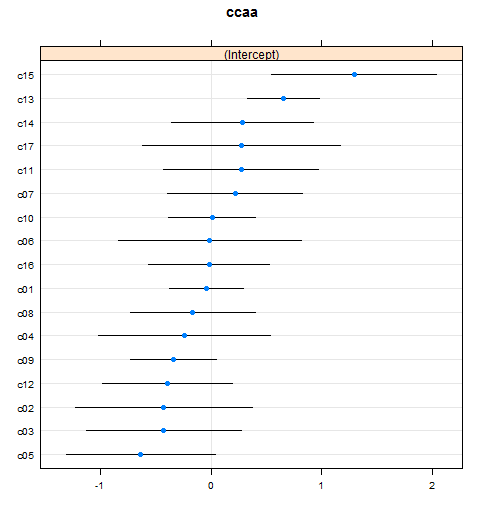
qqmath(ranef(mod.glmer, condVar = TRUE))

y obtener así

y

que vuelven a revelar que gran parte de lo que la autora afirma sobre la confianza es la verbalización de un zumbido browniano.