Incrementalidad via particionamiento recursivo basado en modelos

Planteas un modelo tal como resp ~ treat y no encuentras diferencia significativa. O incluso puede ser negativa. Globalmente.

La pregunta es, con el permiso del Sr. Simpson (o tal vez inspirados por él), ¿existirá alguna región del espacio en la que el tratamiento tiene un efecto beneficioso? Puede que sí. Y de haberla, ¿cómo identificarla?

De eso hablo hoy aquí. E incluyo una protorespuesta.

Primero, genero datos:

n  <- 20000
v1 <- sample(0:1, n, replace = T)
v2 <- sample(0:1, n, replace = T)
v3 <- sample(0:1, n, replace = T)

treat <- sample(0:1, n, replace = T)

y <- v1 + treat * v1 * v2
y <- exp(y) / (1 + exp(y))
y <- sapply(y, function(x) rbinom(1,1,x))

dat <- data.frame(
    y = y,
    treat = factor(treat), v1 = v1,
    v2 = v2, v3 = v3)

Como puede apreciarse, solo las variables v1 y v2 (y no v3) interaccionan con el tratamiento: solo en la región donde v1 = v1 = 1 el efecto del tratamiento es positivo.

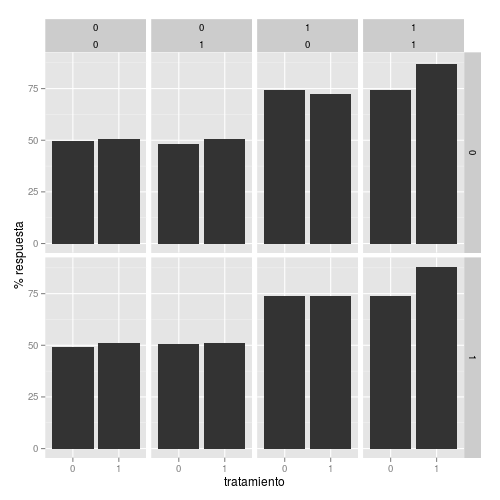
Los datos tienen el siguiente aspecto:

Como se ve, efectivamente, la variable v3 (fila inferior) no tiene ningún efecto; y solo donde v1 = v1 = 1 existe una incrementalidad en el tratamiento.

Ahora,

library(party)
modelo <- mob(y ~ treat | v1 + v2 + v3,
    data = dat, family = binomial())
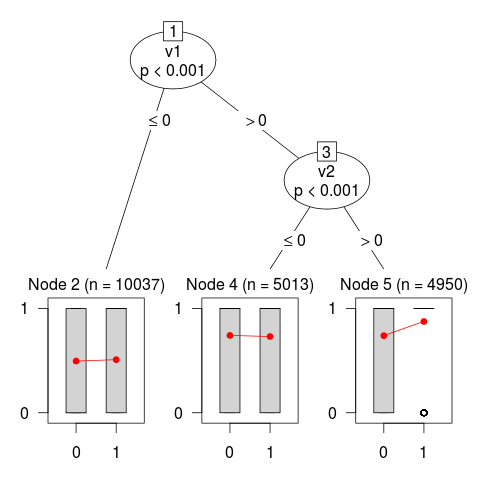
plot(modelo)

hace la magia. El resultado es

que muestra cómo mob ha detectado un efecto diferencial del tratamiento en la región de interés.

Y sí, podría hablar de mob, pero, si os interesa saber más, acudid a lo que sobre la función escribieron sus autores. No tiene desperdicio.