El yuyuplot en perspectiva

El yuyuplot al que me refiero es

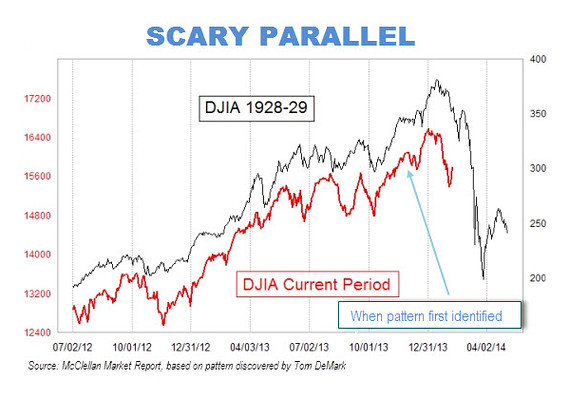
un gráfico ha circulado por internet y que ha causado cierto pánico, se ve (y de ahí el nombre). En algunos sitios —véase este como ejemplo de los menos acertados— se ha intentado de explicar al público sus deméritos.

El mundo de las finanzas debiera ser la envidia de otros ámbitos por el volumen, variedad y velocidad de los datos disponibles en él. Además, desde tiempo atrás, mucho antes de que el siglo nos trajese el big data, la transparencia, el opendetodo y otras concomitancias. A la vez, sin embargo, es inagotable fuente de ejemplos de uso pueril de esos datos. El que nos ocupa es uno de ellos.

El yuyuplot no es otra cosa que una reprensentación prolija y redundante del coeficiente de correlación entre dos segmentos de la misma serie. Esta correlación, de prolongarse en el tiempo —y habida cuenta de lo que sucedió en 1929— implicaría que estamos en la antesala de una debacle bursátil.

Y yo me pregunto lo siguiente:

• ¿Cuántos segmentos —no necesariamente tan eminentes que el de 1929— de la serie temporal del Dow Jones han tenido una correlación elevada con el actual?
• ¿Qué sucedió, p.e., seis meses después con la bolsa?

He querido responderme a mí mismo descargando de aquí las cotizaciones de Dow Jones desde la época de Cánovas y Sagasta y después he ejecutado

dat <- readLines("DJIA.txt")
dat <- dat[-(1:18)]
dat <- gsub("  *", "\t", dat)
dat <- read.table(textConnection(dat), header = T, sep = "\t")

dat$VALUE <- as.numeric(as.character(dat$VALUE))
dat <- subset(dat, !is.na(dat$VALUE))

dat$DATE <- as.Date(as.character(dat$DATE))

base  <- dat$VALUE[dat$DATE >  as.Date("2012-06-30")]
resto <- dat$VALUE[dat$DATE <= as.Date("2012-06-30")]

correlaciones <- sapply(1:(length(resto) - length(base)),
                        function(x) cor(base, resto[x + (1:length(base))])
)

incr.6m <- dat$VALUE[length(base) + 180 + 1:length(correlaciones)]
tmp     <- dat$VALUE[length(base) +       1:length(correlaciones)]
incr.6m <- 100 * (incr.6m - tmp) / tmp

filtro <- correlaciones > 0.8

incrementos <- incr.6m[filtro]
pesos       <- correlaciones[filtro]

library(ggplot2)

tmp <- data.frame(incrementos = incrementos, pesos = pesos / sum(pesos))

ggplot(tmp, aes(x = incrementos, weights = pesos)) +
  geom_density(fill = "blue", alpha = 0.5) +
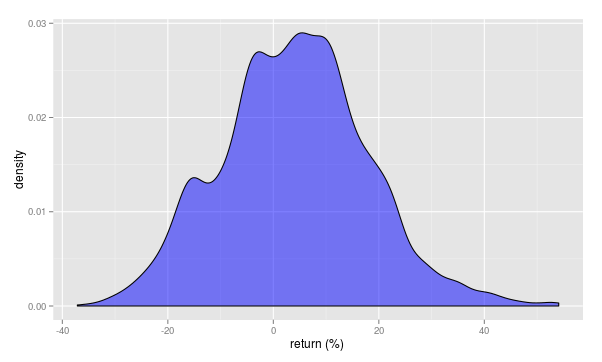
  xlab("return (%) ")

para obtener

Como puede apreciarse y si la historia es tan maestra como cuentan, es más probable que en seis meses la se encuentre por encima que por debajo de las actuales cotizaciones.