Por una vez, accedo a hablar de algo de lo que no sé
Me piden que opine sobre lo de las encuestas electorales y su error. Vaya por delante mi confesión de que de eso sé poco. Soy matemático, no estadístico, y uno de los mayores huecos (¿simas?) de mi formación estadística tiene que ver con todo lo relativo al muestreo. Así que, con la valentía que aporta la ignorancia, procedo.
El primer gran problema con las encuestas electorales es que confunden países con urnas y gente con bolas de colores. Si en una urna hay N bolas (de colores distintos) y queremos estimar su número mediante una extracción de n bolas, existe un margen de error debido a que en lugar de ver todos los datos uno ve únicamente una muestra.
Existe una formulilla que aplican buenamente los responsables de las encuestas que relaciona N con n y que o bien puede consultarse en los libros o bien puede deducirse por ingeniería inversa ajustando una curva a
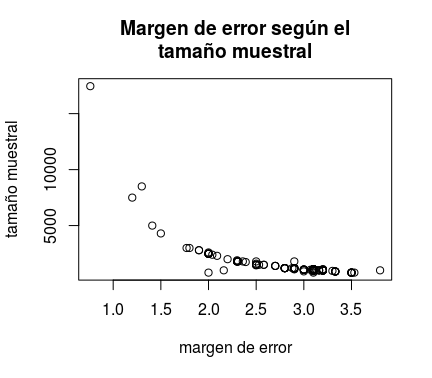
que es una gráfica que muestra la relación entre el tamaño muestral (la n) y el margen de error publicado en una selección de encuestas electorales relativas al 20D (la N es el tamaño total del censo, unos 36.5 millones).
Todas las excusas de malos perdedores que ponen ahora los fabricantes de encuestas (que si la no-respuesta, que si el muestreo, que si…) son todas una. En definitiva, lo que nos están diciendo es que la gente (y lo deberían saber bien porque suelen ser de letras, de los que repiten que las personas son sustancias individuales de naturaleza racional) no son bolas blancas y negras en una urna.
—Doctor, doctor, estas pastillas, ¿me bajarán la fiebre? —Tranquilícese, son efectivas en 9 de cada diez ratoncillos blancos.
Si la respuesta anterior no sería aceptable en boca del médico del seguro, ¿por qué se debería dar como bueno un margen de error diseñado para bolas en urnas y que se aplica a volubles, mendaces y, en ocasiones, inasequibles seres humanos? Sabemos que hay no respuesta; ocultación de voto; categorías de personas que ni tienen fijo, ni responden al móvil ni paran mucho por casa, etc. Entonces, ¿por qué se hace como si no?
En lugar de rematar una encuesta electoral con esa coletilla seudocientífica de que partiendo de los criterios del muestreo aleatorio simple [!!!!], para un nivel de confianza del 95.5% (que es el habitualmente adoptado) y en la hipótesis más desfavorable de máxima indeterminación (p=q=50), el margen de error de los datos referidos al total de la muestra es de ± 2.9 puntos, deberían ser más honestos y decir algo así:
En encuestas realizadas con metodologías y tamaños muestrales similares en contextos comparables, la distribución del error cometido con respecto a los resultados finales siguieron la distribución que indica el histograma adjunto. En un 80% de los casos el error ha sido inferior al 7%, aunque no son del todo infrecuentes (5%) errores superiores al 10%.
Tenemos un histórico de encuestas y errores suficiente como para computar empíricamente (en lugar de con una fórmula tonta de Excel) el error que se puede llegar a esperar.
Mi segundo comentario es que, aunque a los sociólogos de la cocina de las encuestas Bayes les suene a aspirinas con aliteración de ese, lo son profundamente en la práctica. La llamada cocina de las encuestas no es sino el arrejuntamiento de una serie de hipótesis cualitativas de partida, i.e., una especie de a priori en alpargatas, con los datos del call center. Esto, de nuevo, tendería a ensanchar el error: posiblemente haya en esta operación algo de bias-variance trade-off.
No seré yo el que lo haga y menos en estos términos: los sorprendentes resultados electorales han atemperado mi interés por reconvertirme en estudiante pobre en una suerte de autoexilio interior en lugar de continuar como autónomo currante, cotizante e irrepefeacoquinante. Pero tal vez a otro le interese.
Y relacionado con lo anterior y por concluir, habría que pensar en algún tipo de efecto anchoring o priming. Esto es altamente especulativo y debería meterme dentro de la cabeza de uno de esos señores que llevan toda la semana buscando excusas para saber cómo operan realmente en la cocina de las encuestas. Pero no es descabellado pensar que unos y otros se miran de reojo y que una vez que uno dice 7, el de enfrente prefiere 7.5 a 9, diga lo que diga el call center, porsiaca.

