Grafos sobre mapas
He escrito de grafos, he escrito de mapas; hoy hablaré de la combinación de ambas cosas.
Tengo un grafo cuyos nodos están geoposicionados. Lo quiero estudiar utilizando herramientas de grafos (vía igraph) pero después representarlos sobre una capa con información geográfica (una foto satelital de Google Maps, vamos).
La red va a ser la de guifi.net en los derredores de Barcelona. guifi.net es un proyecto para crear una red de telecomunicaciones mancomunada, abierta, libre y neutral. Quienes forman parte de ella colocan antenas que se conectan con otras de la red y comienzan en enviar bits. Las antenas y sus conexiones conforman una red que se puede estudiar como cualquier otra: ¿qué nodos/enlaces son más centrales/críticos? Etc.
En este primer pedazo de código voy a descargar de los servidores de guifi.net el fichero CNML (un dialecto de XML) que describe la estructura de la red en la zona de interés:
library(XML)
library(plyr)
library(igraph)
library(ggmap)
library(popgraph)
tmp <- readLines("https://guifi.net/en/guifi/cnml/2435/detail")
tmp <- xmlParse(tmp)
nodos <- xpathApply(tmp, "//*/node")
lista.nodos <- rbind.fill(lapply(
nodos, function(x) data.frame(t(xmlAttrs(x)),
stringsAsFactors = FALSE)))
lista.links <- lapply(nodos, function(x){
from <- xmlAttrs(x)["id"]
to <- xpathApply(x, ".//link", xmlAttrs)
if (length(to) == 0)
return(NULL)
to <- sapply(to, function(x) x["linked_node_id"])
data.frame(from = from, to = to, stringsAsFactors = FALSE)
})
lista.links <- do.call(rbind, lista.links)
lista.links <- lista.links[lista.links$from %in% lista.nodos$id,]
lista.links <- lista.links[lista.links$to %in% lista.nodos$id,]
lista.links <- lista.links[lista.links$to != lista.links$from,]A continuación voy a crear la red, recuperar la componente conexa principal (ignorando nodos aislados, etc.) y calcular algunas estadísticas de interés (el famoso betweenness):
g <- graph.data.frame(lista.links, directed = F, lista.nodos)
g.working <- subgraph(g, V(g)$status %in% c("Working"))
# si quieres representarlo, descomenta:
#my_layout <- layout.fruchterman.reingold(g.working)
#plot(g.working, layout = my_layout, vertex.label = NA, vertex.size = 0.3)
# mayor componente conexa
kk <- clusters(g.working)
g.wc <- subgraph(g.working, kk$membership == 1)
g.wc <- set.edge.attribute(g.wc, name = "betweenness", E(g.wc),
edge.betweenness(g.wc))
g.wc <- set.vertex.attribute(g.wc, name = "btw",
V(g.wc), betweenness(g.wc))Podemos representar la red con
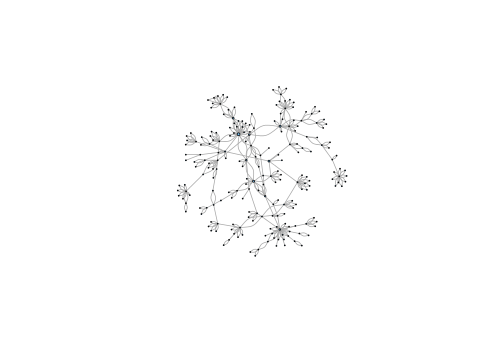
my_layout <- layout.fruchterman.reingold(g.wc)
plot(g.wc, layout = my_layout, vertex.label = NA,
vertex.size = (1 + V(g.wc)$btw) / 3000)para obtener
pero podemos usar otro layout geográfico para situar cada punto… donde está, es decir, hacer
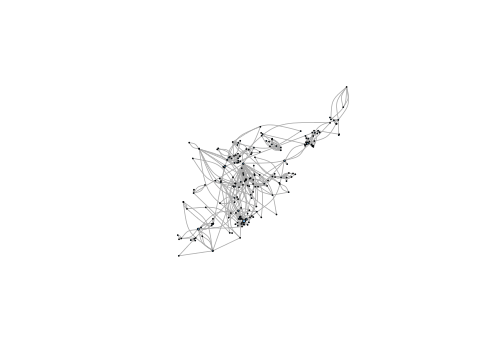
geom.layout <- cbind(as.numeric(V(g.wc)$lon),
as.numeric(V(g.wc)$lat))
plot(g.wc, layout = geom.layout, vertex.label = NA,
vertex.size = (1 + V(g.wc)$btw) / 3000)para obtener
y ver cómo, por ejemplo, nodos con una centralidad (y criticidad) elevada están en el enlace principal entre Barcelona y Badalona. O eso es lo que parece porque, bueno, nos faltan todas las referencias geográficas.
En lo que sigue voy a representar esa red sobre una capa con referencias geográficas usando ggmap y un paquete oscuro, [popgraph](http://cran.r-project.org/web/packages/popgraph/index.html), que hace muchas más cosas de las que anuncia.
(Nota: esta es una peculiaridad muy irritante de R y de su comunidad sobre la que volveré pronto).
Así que
map.bcn <- get_map("Barcelona", maptype="satellite", zoom = 12)
tmp <- as.popgraph(g.wc)
tmp <- set.vertex.attribute(tmp, name = "Longitude", V(tmp),
value = as.numeric(V(tmp)$lon))
tmp <- set.vertex.attribute(tmp, name = "Latitude", V(tmp),
value = as.numeric(V(tmp)$lat))
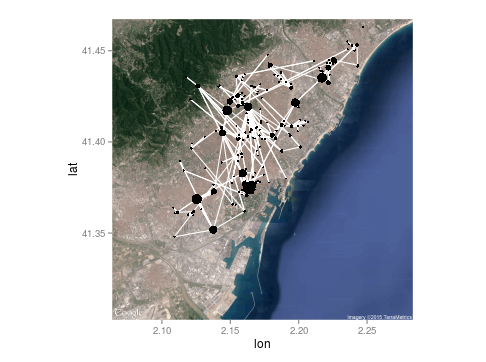
p <- ggmap(map.bcn)
p <- p + geom_edgeset(aes(x = Longitude, y = Latitude), tmp, color="white" )
p <- p + geom_nodeset(aes(x = Longitude, y = Latitude, size = btw), tmp)
py obtengo
Notas adicionales:
- He usado parámetros gráficos por defecto. El resultado podía haber sido más resultón si no escribiese a matacaballo.
- Los detractores de
ggmapy sus concomitancias podrán felicitarse al saber que también es posible resolver el problema anterior usando[Raster*](http://cran.r-project.org/web/packages/raster/index.html)y demás.