No me ha salido, pero lo cuento igual
Creo que todos sabéis la historia de las admisiones de la Universidad de Berkeley y la paradoja de Simpson. Con palabras, muchas palabras, está contado, por ejemplo, aquí. Y si buscáis ubc admissions simpson en Google la encontraréis también en modo --verbose en muchos más sitios.
En R puede resumirse en
library(reshape2)
library(plyr)
data(UCBAdmissions)
raw <- as.data.frame(UCBAdmissions)
dat <- dcast(raw, Gender + Dept ~ <a href="http://inside-r.org/packages/cran/AdMit">Admit)
mod.0 <- glm(cbind(Admitted, Rejected) ~ Gender, data = dat, family = binomial)
mod.1 <- glm(cbind(Admitted, Rejected) ~ Gender + Dept, data = dat, family = binomial)Echad un vistazo a los coeficientes de Gender en ambos modelos y veréis.
Lo que se me ha ocurrido es lo siguiente. Imaginad que hombres y mujeres solicitan admisiones a esos departamentos sin que el sexo induzca sesgo alguno en las preferencias. Por su parte, los departamentos aceptan o rechazan candidatos en proporciones fijas (e iguales a las del caso que nos ocupa).
De otra manera, un candidato tiene una probabilidad $latex p_H$ de ser hombre, una probabilidad $latex P_{Di}$ de solicitar la admisión en el departamento $latex i$ y una probabilidad $latex p_{Ai}$ de ser admitido en él.
La idea es comparar las regresiones logísticas anteriores: una que incluya Dept y la otra no. Lo que yo esperaba es que los coeficientes de Gender en muchas simulaciones:
- Estuviesen centrados en cero en ambos casos: por construcción, el efecto del sexo es nulo.
- Que la varianza del del modelo que incluye
Deptfuese menor. Esto está inspirado por el ejemplo anterior. En los casos en que por efecto del muestreo haya un desequilibrio por sexos en las solicitudes a los distintos departamentos —como ocurrió en el ejemplo con el que abro la entrada—, controlar porGenderayudaría a corregir el sesgo. Reducir el sesgo en cada simulación conlleva reducir la varianza global, ¿no?
Pues parece que algo se me ha escapado porque, salvo error u omisión,
accept.rate <- dcast(raw, Dept ~ <a href="http://inside-r.org/packages/cran/AdMit">Admit, fun.aggregate = sum, value.var = "Freq")
accept.rate$size <- accept.rate$Admitted + accept.rate$Rejected
accept.rate$rate <- accept.rate$Admitted / accept.rate$size
gender.rate <- melt(dat)
gender.rate <- tapply(gender.rate$value, gender.rate$Gender, sum)
extract.coefs <- function(accept.rate, gender.rate){
Gender <- sample(names(gender.rate), sum(gender.rate),
prob = gender.rate / sum(gender.rate), replace = T)
Dept <- sample(accept.rate$Dept, sum(gender.rate),
prob = accept.rate$rate, replace = T)
Admitted <- accept.rate$rate[match(Dept, accept.rate$Dept)]
Admitted <- runif(length(Admitted)) < Admitted
dat <- data.frame(Gender = Gender, Dept = Dept, Admitted = Admitted)
dat <- ddply(dat,
.(Gender, Dept), summarize,
Rejected = sum(!Admitted), Admitted = sum(Admitted))
mod.0 <- glm(cbind(Admitted, Rejected) ~ Gender, data = dat,
family = binomial)
mod.1 <- glm(cbind(Admitted, Rejected) ~ Gender + Dept, data = dat,
family = binomial)
c(coefficients(mod.0)[2], coefficients(mod.1)[2])
}
res <- replicate(1000, extract.coefs(accept.rate, gender.rate))
res <- as.data.frame(t(res))
colnames(res) <- c("mod0", "mod1")
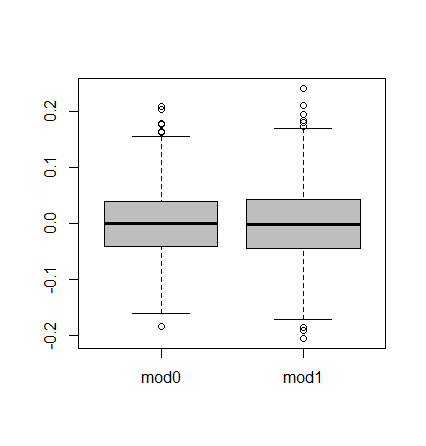
boxplot(res, col = "gray")produce
justo al contrario de lo esperado. ¡Carajo!
P.D.: ¿Igual n es demasiado grande como para que se manifiesten las ventajas de controlar por Dept?