Para que copien, peguen y disfruten: addenda

Ayer dejé publicadas unas cuantas líneas de R y la promesa de contar de qué iba la cosa. Adelantando acontecimientos, he recibido comentarios públicos y privados al respecto que en esta entrada trataré de contestar.

El código era, una vez mínimamente desofuscado (no quería dar demasiadas pistas):

vertice.x <- c(0,1,2)                            # 1
vertice.y <- c(0,1,0)                            # 2
muestra <- sample( 1:3, 100000, replace = T )    # 3
iter <- function( ini, v ){                      # 4
   out <- rep( ini, length(v) )                  # 5
   for( i in 2:length(v) )
      out[i] <- ( out[i-1] + v[i] ) / 2          # 6
   out
}
plot( iter( runif(1), v.x[ muestra ] ),
      iter( runif(1),  v.y[ muestra ] ), pch = "." )

He aquí lo que hace:

1. Asigna a una variable las coordenadas x de un triángulo.
2. Asigna a otra variable las coordenadas y del triángulo.
3. Selecciona una muestra aleatoria de tamaño 100.000 (con reemplazo, obviamente) de los vértices de dicho triángulo.
4. Crea una función, iter, que calcula iterativamente una sucesión de puntos.
5. La función genera una sucesión de puntos comenzando por uno al azar. Por eficiencia, es mejor asignar espacio previamente. En este caso es un vector de longitud igual al de la muestra de puntos.
6. El bucle calcula de hecho la sucesión de puntos. Cada uno de ellos es el punto medio entre el anterior anterior y el vértice (elegido al azar, recordemos) correspondiente. Por lo tanto, la sucesión de puntos trata de acercarse a los vértices del triángulo en una especie de caminata aleatoria sin en realidad llegar a poder alcanzar jamás ninguno de ellos. (Supogo que este algoritmo le habría quitado el sueño malamente al pobre Zenón).

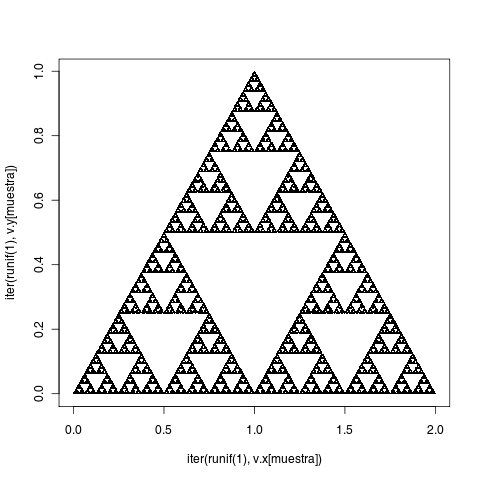
Finalmente, se representan los puntos gráficamente en el plano. El resultado, como todo antento lector de las páginas 42 a 45 de este libro debería haber reconocido, es el triángulo de Sierpinsky (como dice el autor del libro, el resultado es dicho triángulo querámoslo o no).

Y cierro la entrada para protestar amargamente por el hecho de que en Colombia uno pueda comprar cualquier libro editado por cualquier universidad de país en un único portal y en la madre patria, tan civilizada que hasta nos da la libertad de fumar en las cafeterías, no.