Reconstrucción de una distribución a partir de un histograma

2025-12-2 (Última modificación: 2025-11-29)

Un viejo amigo me escribe y me propone (simplificándolo) el siguiente problema:

Tengo una normal de parámetros desconocidos.
De ella solo dispongo de un histograma.
¿Cómo puedo reconstruir la normal original? Es decir, ¿cómo puedo estimar los $\mu$ y $\sigma$ originales?

En el caso concreto, la normal tiene una media próxima a 255 y los valores del histograma proceden de una muestra suya redondeada al entero más próximo.

Aquí va mi solución.

Se trata de un problema de libro en el que hay un modelo generativo detrás de la muestra.

Una normal desconocida pero fija genera números.
Estos se aproximan al entero más próximo.

Se trata de invertir el proceso. Para ello:

Consideraremos una priori más o menos razonable para los datos en cuestión. Sabemos que la media no puede estar muy lejos de 255 y que la varianza es relativamente pequeña: tolera errores de un tamaño 2 o 3 como mucho. Esta priori, por supuesto, no sale de la nada: está relacionada con lo que me han contado sobre el problema concreto que quiero resolver.
Construiremos el proceso generativo.
Muestrearemos la posteriori de los parámetros $\mu$ y $\sigma$ de la normal original.

Primero, los valores reales de los parámetros desconocidos:

mu <- 255.5
sigma <- 1.2

Luego, el histograma (simulado):

muestra <- rnorm(n, mu, sigma)
muestra <- round(muestra)

densidad <- table(muestra) / length(muestra)

densidad <- data.frame(
  index = as.integer(names(densidad)),
  prob  = as.numeric(densidad)
)

Que tiene este aspecto:

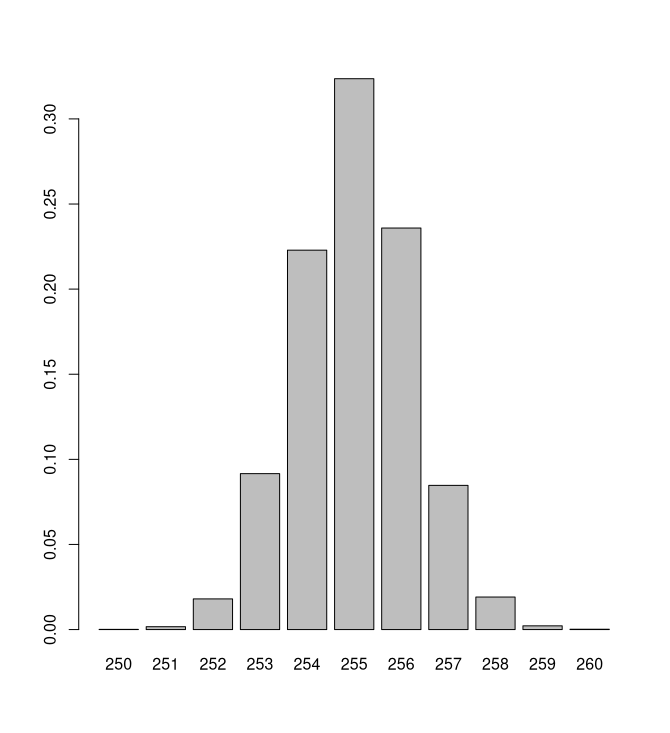
Como prioris de $\mu$ y $\sigma$ voy a considerar distribuciones normales de parámetros 255 y 10 y gamma de parámetros 3.75 y 2.5:

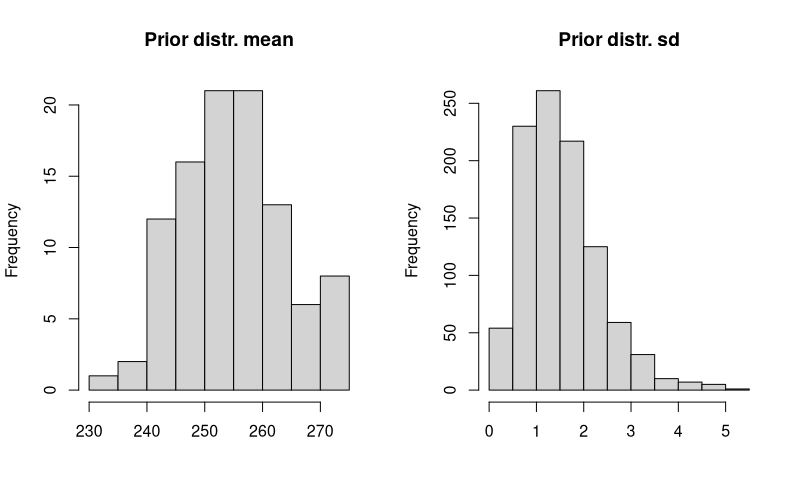
(prometo que lo que se representa en el histograma izquierdo no es otra cosa que x1 <- rnorm(100, 255, 10).)

Finalmente, muestreo la posteriori usando el método del rechazo (la posteriori es la priori multiplicada por el histograma):

sample_posterior <- function() {

  # sample prior
  mu_prior <- rnorm(1, 255, 10)
  sigma_prior <- rgamma(1, 3.75, 2.5)
  candidate <- rnorm(1, mu_prior, sigma_prior)

  # generate the "round value"
  histogram_candidate <- round(candidate)

  # look for the candidate in the histogram
  if (! histogram_candidate %in% densidad$index )
    return(sample_posterior())

  # if found, reject it according to the density values
  if (runif(1) > densidad$prob[densidad$index == histogram_candidate])
    return(sample_posterior())

  # if all goes well, accept the prior sample
  return(c(mu_prior, sigma_prior))

}

muestras_posterior <- replicate(1000, sample_posterior())

mu_posterior <- muestras_posterior[1,]
sigma_posterior <- muestras_posterior[2,]

Finalmente,

mp0 <- data.frame(
  value = rnorm(1000, 255, 10),
  class = "prior"
)

tmp1 <- data.frame(
  value = mu_posterior,
  class = "posterior"
)

tmp <- rbind(tmp0, tmp1)

ggplot(tmp, aes(x = value, fill = class)) +
  geom_density(alpha = .5) +
  theme_bw()

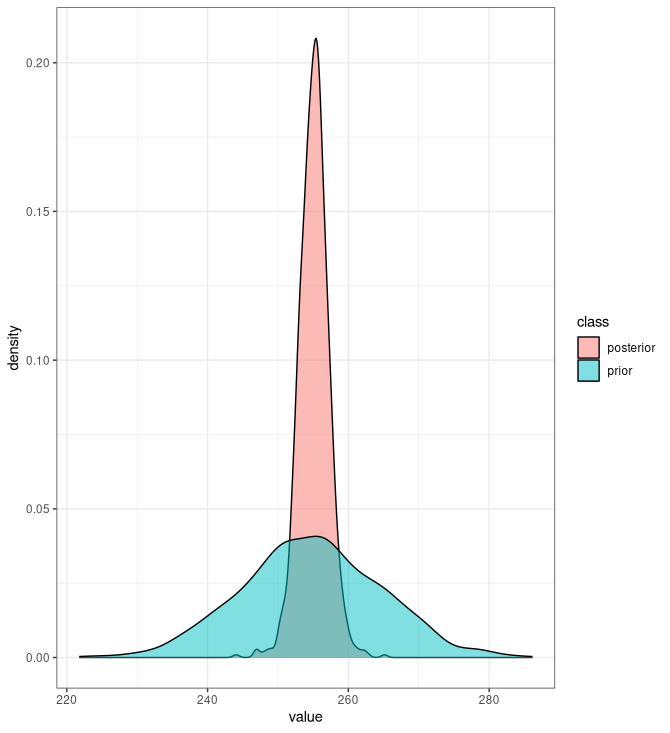
Lo cual pone irrefutablemente de manifiesto cómo me infravalora la economía española circa 2025.