Gestión de la mendacidad encuestoelectoral: los números

Continuando con la entrada anterior, ahora, números.

Primero, el planteamiento (cuatro partidos, etc.):

probs <- c(4, 3, 2, 1)
probs <- probs / sum(probs)
partidos <- letters[1:length(probs)]

Nos hará falta más adelante

library(plyr)
library(rstan)
library(ggplot2)
library(reshape2)

Sigo con el proceso de muestreo. Reitero: cada encuestador enseña al encuestado una tarjeta al azar donde aparece el nombre de dos partidos y le pregunta si ha votado (o piensa votar) a alguno de ellos.

n <- 3000
resultados <- data.frame(tarjeta = sample(1:nrow(tarjetas), n, replace = T), 
                         partido = sample(partidos, n, prob = probs, replace = T))
resultados <- data.frame(tarjetas[resultados$tarjeta,], partido = resultados$partido)
resultados$coincide <- resultados$partido == resultados$partido1 | 
  resultados$partido == resultados$partido2
 
# proporciones reales en la muestra
props.muestra <- table(resultados$partido) / nrow(resultados)
 
# resultados agregados (por tarjeta)
resultados.agg <- ddply(resultados, .(partido1, partido2), 
                    summarize, 
                    total = length(partido1), 
                    coincidencias = sum(coincide))

codigo <- '
data {
  int<lower=1> N;
  int partido1[N];
  int partido2[N];
  int total[N];
  int coincidencias[N];
  int <lower = 1> n_partidos;
}
 
parameters {
  simplex[n_partidos] pes; //probabilidades
}
 
model {
  // dejamos la priori a "la cocina"
 
  // verosimilitud
  for (i in 1:N){
    coincidencias[i] ~ binomial(total[i], pes[partido1[i]] + pes[partido2[i]]);
  }
}
'
 
fit <- stan(model_code = codigo, 
            data = list(n_partidos = length(partidos),
                        N = nrow(resultados.agg),
                        partido1 = match(resultados.agg$partido1, partidos),
                        partido2 = match(resultados.agg$partido2, partidos),
                        total = resultados.agg$total,
                        coincidencias = resultados$coincidencias), 
            iter=12000, warmup=2000, 
            chains=2, thin=10)
 
res <- as.data.frame(fit)[,1:length(partidos)]
colnames(res) <- partidos
res <- melt(res)
colnames(res) <- c("partido", "pct")
 
ggplot(res, aes(x = pct, fill = partido)) + 
  geom_density(alpha = 0.3) + ylab("")

produce

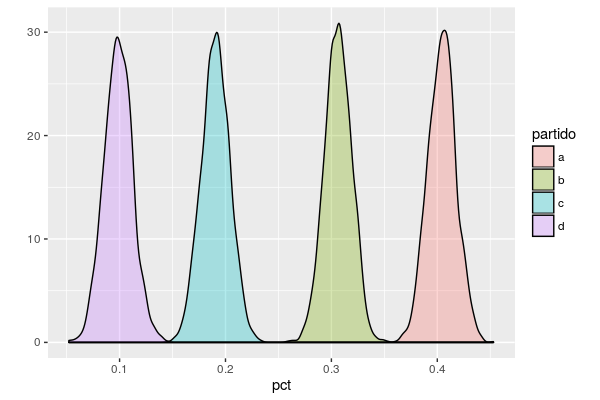
partidos_tarjetas

que no está mal del todo.

En otra entrada, si procede, la comparación con el método normal para ver cómo se ensanchan (relativamente) los intervalos de confianza.