Coaliciones de Banzhaf en el 20D
Usando código de una entrada anterior voy a medir el poder de cada partido político de acuerdo con Banzhaf tras las elecciones de diciembre de 2015.
escannos <- c(123, 90, 69, 40, 9, 8, 6, 2, 2, 1)
names(escannos) <- c( "pp", "psoe", "pod", "c's",
"erc", "dl", "pnv", "iu", "bildu", "cc")
banzhaf(escannos)da 14 coaliciones mínimas,
pp psoe
pp pod
pp c's erc dl
pp c's erc pnv
pp c's erc iu bildu
pp c's dl pnv
pp c's dl iu bildu cc
psoe pod c's
psoe pod erc dl
psoe pod erc pnv iu
psoe pod erc pnv bildu
psoe pod dl pnv iu bildu
psoe pod dl pnv iu cc
psoe pod dl pnv bildu ccy un reparto de poder que queda de esta manera:
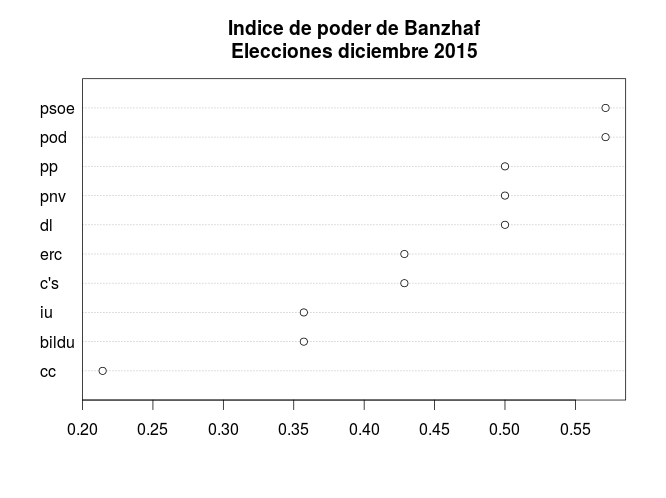
psoe pod pp pnv dl erc c's iu bildu cc
57.1 57.1 50.0 50.0 50.0 42.8 42.8 35.7 35.7 21.4Gráficamente,
Y una nota: coaliciones mínimas no significa coaliciones probables; de hecho, obviamente, las hay imposibles.